
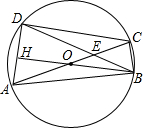
 如图,四边形ABCD内接于⊙O,对角线AC经过圆心O.且交BD于点E,BO⊥AD于点H,OA=AD=2,则OE:EC值是( )
如图,四边形ABCD内接于⊙O,对角线AC经过圆心O.且交BD于点E,BO⊥AD于点H,OA=AD=2,则OE:EC值是( )| A. | 1:2 | B. | 1:$\sqrt{2}$ | C. | 1:$\sqrt{3}$ | D. | $\sqrt{2}$:$\sqrt{3}$ |
分析 首先利用勾股定理求出DC,再根据BO∥DC,得$\frac{OE}{EC}$=$\frac{OB}{DC}$即可解决问题.
解答 解: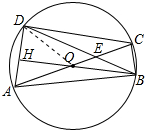 如图连接OD,
如图连接OD,
∵OA=OD=AD=2,
∴△AOD是等边三角形,
∴∠DAO=90°,
∵AC是直径,
∴∠ADC=90°,∠ACD=30°,
∴DC=$\sqrt{A{C}^{2}-A{D}^{2}}$=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$.
∵BO⊥AD,CD⊥AD,
∴BO∥DC,
∴$\frac{OE}{EC}$=$\frac{OB}{DC}$=$\frac{2}{2\sqrt{3}}$=$\frac{1}{\sqrt{3}}$.
故选C.
点评 本题考查平行线分线段成比例定理、圆的有关知识,解题的关键是发现OB∥DC,把$\frac{OE}{EC}$转化为$\frac{OB}{DC}$,学会转化的思想,属于中考常考题型.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
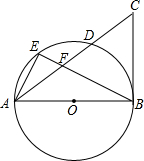 如图,AB是⊙O的直径,BC是⊙O的切线,连接AC交⊙O于点D,E为$\widehat{AD}$上一点,连结AE、BE,BE交AC于点F,且∠AFE=∠EAB.
如图,AB是⊙O的直径,BC是⊙O的切线,连接AC交⊙O于点D,E为$\widehat{AD}$上一点,连结AE、BE,BE交AC于点F,且∠AFE=∠EAB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
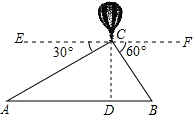 如图所示,从热气球C上测定建筑物A、B底部的俯角分别为30°和60°,已知AB间的距离为180米,CD垂直于AB于点D.问:此时热气球的高度为多少?
如图所示,从热气球C上测定建筑物A、B底部的俯角分别为30°和60°,已知AB间的距离为180米,CD垂直于AB于点D.问:此时热气球的高度为多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com