
����Ŀ����ͼ������ABCD�У�AB=13��BC=50��BC���ϵĸ�Ϊ12����P�ӵ�B��������B��A��D��A�˶�����B��A�˶�ʱ���ٶ�Ϊÿ��13����λ���ȣ���A��D��A�˶�ʱ���ٶ�Ϊÿ��8����λ���ȣ���Q�ӵ� B������BC�����˶����ٶ�Ϊÿ��5����λ���ȣ�P��Q����ͬʱ����������Q�����Cʱ��P��Q����ͬʱֹͣ�˶������P���˶�ʱ��Ϊt���룩������PQ��
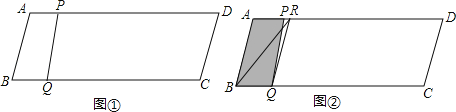
��1������P��A��D��A�˶�ʱ����AP�ij����ú�t�Ĵ���ʽ��ʾ����
��2������AQ���ڵ�P��B��A��D�˶������У�����P���B����A���غ�ʱ������APQ�����ΪS����S��t֮��ĺ�����ϵʽ��
��3������Q��QR��AB����AD�ڵ�R������BR����ͼ�����ڵ�P��B��A��D�˶������У����߶�PQɨ����ͼ�Σ���Ӱ���֣����߶�BR�ֳ������ȵ�������ʱt��ֵ��
��4�����C��D����ֱ��PQ�ĶԳƵ�ֱ�ΪC�䡢D�䣬ֱ��д��C��D����BCʱt��ֵ��
���𰸡���1��108��8t��
��2��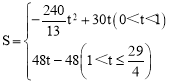 ��
��
��3����t=1��![]() ʱ���߶�PQɨ����ͼ�Σ���Ӱ���֣����߶�BR�ֳ������ȵ���������
ʱ���߶�PQɨ����ͼ�Σ���Ӱ���֣����߶�BR�ֳ������ȵ���������
��4����t=7��t=![]() ��t=
��t=![]() ʱ����C��D����ֱ��PQ�ĶԳƵ�ֱ�ΪC�䡢D�䣬��C��D����BC��
ʱ����C��D����ֱ��PQ�ĶԳƵ�ֱ�ΪC�䡢D�䣬��C��D����BC��
��������
������1�����������������P��A��D�˶�ʱ������P��D��A�˶�ʱ�ֱ���Ա�ʾ��AP��ֵ��
����P��A��D�˶�ʱ��AP=8��t��1��=8t��8��
����P��D��A�˶�ʱ��AP=50��2��8��t��1��=108��8t��
��2��������������0��t��1ʱ����1��t��![]() ʱ�����������ε������ʽ�ֱ����S��t�ĺ�����ϵʽ��
ʱ�����������ε������ʽ�ֱ����S��t�ĺ�����ϵʽ��
����P���A�غ�ʱ��BP=AB��t=1��
����P���D�غ�ʱ��AP=AD��8t��8=50��t=![]() ��
��
��0��t��1ʱ����ͼ��

������Q��QE��AB�ڵ�E��
S��ABQ=![]() ��
��
��![]() ��
��
��![]() ��
��
��S=![]() ��
��
��1��t��![]() ʱ����ͼ��
ʱ����ͼ��
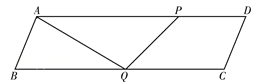
S=![]() ��
��
���������� 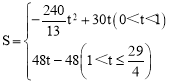 ��
��
��3��������������0��t��1ʱ����1��t��![]() ʱ����
ʱ����![]() ��t��
��t��![]() ʱ�����������ε������Ƚ������������⼴����
ʱ�����������ε������Ƚ������������⼴����
��P���R�غ�ʱ��AP=BQ��8t��8=5t��t=![]() ��
��
��0��t��1ʱ����ͼ��

��S��BPM=S��BQM����PM=QM��
��AB��QR��
���PBM=��QRM����BPM=��MQR��
����BPM����RQM��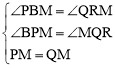 ��
��
���BPM�ա�RQM��AAS������BP=RQ��
��RQ=AB����BP=AB��
��13t=13����ã�t=1��
��1��t��![]() ʱ����ͼ��
ʱ����ͼ��

��BRƽ����Ӱ�����������P���R�غϡ�
��t=![]() ��
��
��![]() ��t��
��t��![]() ʱ����ͼ��
ʱ����ͼ��
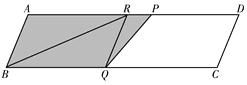
��S��ABR=S��QBR����S��ABR��S�ı���BQPR��
��BR���ܰ��ı���ABQP�ֳ������ȵ������֡�
��4������������
��P��A��D֮���D��A֮����C��D����BC�Ϸ���C��D����BCʱ����ͼ��
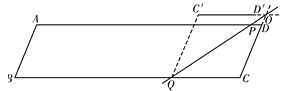
���C��OQ=��OQC��
�ߡ�C��OQ�ա�COQ�����C��OQ=��COQ��
���CQO=��COQ����QC=OC��
��50��5t=50��8��t��1��+13��
��50��5t=8��t��1����50+13��
��ã�t=7��t=![]() ��
��
��P��A��D֮���D��A֮�䣬C��D����BC�·���C��D����BCʱ����ͼ��

ͬ�������ε����ʿ��Եó���OD=PD��
��50��5t+13=50��8��t��1����
��50��5t+13=50����108��8t����
50��5t+13=50��8��t��1���⣻
��50��5t+13=50����108��8t����ã�t=![]() ��
��
������������t=7��t=![]() ��t=
��t=![]() ʱ����C��D����ֱ��PQ�ĶԳƵ�ֱ�ΪC�䡢D�䣬��C��D����BC��
ʱ����C��D����ֱ��PQ�ĶԳƵ�ֱ�ΪC�䡢D�䣬��C��D����BC��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У����ڵ�P(x��y)�����ǰѵ�![]() (-y+1��x+1)������P�����.��֪��A1�İ����ΪA2����A2�İ����ΪA3����A3�İ����ΪA4�������������εõ���A1��A2��A3������An����.����A1������Ϊ(2��4)����A2017������Ϊ ( )
(-y+1��x+1)������P�����.��֪��A1�İ����ΪA2����A2�İ����ΪA3����A3�İ����ΪA4�������������εõ���A1��A2��A3������An����.����A1������Ϊ(2��4)����A2017������Ϊ ( )
A. (-3��3) B. (-2��-2) C. (3��-1) D. (2��4)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������AM��BN���߶�CD�������˵�C��D�ֱ�������BN��AM�ϣ��ҡ�A����BCD��108�㣮E���߶�AD��һ�㣨�����A��D�غϣ�����BDƽ�֡�EBC��
��1�����ABC�Ķ�����
��2������ͼ���ҳ����ABC��ȵĽǣ���˵�����ɣ�
��3����ƽ���ƶ�CD����AD��CD�����ADB���AEB�Ķ���֮���Ƿ�����CDλ�õı仯�������仯�����仯���ҳ��仯���ɣ������䣬��������ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
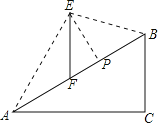
����Ŀ����ͼ�����¶�![]() ��
��![]() ��б��AB������һ���߸�EF������ʦ�ڵ�A�����E������Ϊ
��б��AB������һ���߸�EF������ʦ�ڵ�A�����E������Ϊ![]() ����б��ǰ��20����B����ʱ��õ�E������Ϊ
����б��ǰ��20����B����ʱ��õ�E������Ϊ![]() ����Ҫ��б��AB����һ��P����P����װһ������PE���̶����߸ˣ���ʹEF������ֱ��Ϊʹ����PE��̣���FP�ij���ԼΪ
����Ҫ��б��AB����һ��P����P����װһ������PE���̶����߸ˣ���ʹEF������ֱ��Ϊʹ����PE��̣���FP�ij���ԼΪ![]() �ο����ݣ�
�ο����ݣ�![]()
A. ![]() �� B.
�� B. ![]() �� C.
�� C. ![]() �� D.
�� D. ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ABC���������������ֱ�ΪA����5��0����B����2��3����C����1��0��
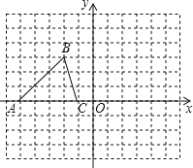
��1��������ABC����ƽ��3����λ�ġ�A1B1C1��
��2������A1B1C1��ԭ��O��ת180�㣬������ת��ġ�A2B2C2��
��3���ڣ�2���У��߶�A1B1 ɨ�������Ϊ�� �� ������ͼ��С�����ı߳�Ϊ1����λ���ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
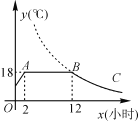
����Ŀ������ij�߲��������������½ϵ�ʱ����װ�к���ϵͳ�Ĵ�������һ������Ȼ�������¶�Ϊ18 �������������������Ʒ�֣���ͼ��ij�����ϵͳ�ӿ������رռ��رպ������¶�y(��)��ʱ��x(Сʱ)�仯�ĺ���ͼ������BC����˫����y=![]() ��һ���֣������ͼ����Ϣ����������⣺
��һ���֣������ͼ����Ϣ����������⣺
(1)����ϵͳ�����챣�ִ������¶�18 ���ʱ���ж���Сʱ��
(2)��k��ֵ��
(3)��x��16ʱ�������ڵ��¶�ԼΪ���ٶȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������:�١�1=��3,�ڡ�2+��4=180�����ۡ�4=��5,�ܡ�2=��3,�ݡ�6=��2+��3�����ж�ֱ��l1��l2�ĸ����ǣ� ��

A. 5B. 4C. 3D. 2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Rt��ABC�У���ACB��90������A��30����BC��3cm������P�ӵ�A��������AB������ÿ��2cm���ٶ����յ�B�˶���ͬʱ������Q�ӵ�B������BC������ÿ��1cm���ٶ����յ�C�˶�������PQC���ۣ���P�Ķ�Ӧ��ΪR�����Q�˶���ʱ��Ϊt�룬���ı���PCRQΪ���Σ���t��ֵΪ��������

A. ![]() B. 2C. 1D.
B. 2C. 1D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
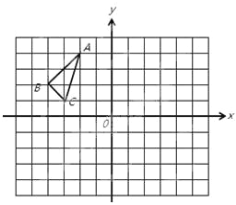
����Ŀ����ABC ��ƽ��ֱ������ϵ�е�λ����ͼ��ʾ�� ����ÿ��С�����εı߳�Ϊ1����λ���ȣ�
��1����ABC ����ԭ�� O �����ĶԳ�ͼ��Ϊ��A1B1C1��д���� A �Ķ�Ӧ�� A1 ������ ��
��2����������ABC �Ƶ�O ˳ʱ����ת 90���õ��ġ�A2B2C2��
��3���� P��a��b��Ϊ��ABC ����һ�㣬���ڡ�A2B2C2 �У��� P ��Ӧ�ĵ� Q ������Ϊ ��
��4����ֱ��д������ A��B��C Ϊ�����ƽ���ı��εĵ��ĸ����� D ������ ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com