
如图,在△ABC中,AB=AC,D、E是△ABC内两点,AD平分∠BAC,∠EBC=∠E=60°,若BE=6cm,DE=2cm,则BC=_________ .
8cm.
解析试题分析:首先延长ED交BC于M,延长AD交BC于N,过点D作DF∥BC,交BE于F,易得:△EFD∽△EBM,又由AB=AC,AD平分∠BAC,根据等腰三角形的性质,即可得AN⊥BC,BN=CN,又由∠EBC=∠E=60°,可得△BEM与△EFD为等边三角形,又由直角三角形中,30°角所对的直角边是斜边的一半,即可求得MN与BM的值,继而求得答案.
试题解析:延长ED交BC于M,延长AD交BC于N,过点D作DF∥BC,交BE于F,
可得:△EFD∽△EBM,
∵AB=AC,AD平分∠BAC,
∴AN⊥BC,BN=CN,
∵∠EBC=∠E=60°,
∴△BEM为等边三角形,
∴△EFD为等边三角形,
∵BE=6cm,DE=2cm,
∴DM=4cm,
∵∠DNM=90°,∠DMN=60°,
∴∠NDM=30°,
∴NM= DM=2cm,
DM=2cm,
∴BN=BM-MN=6-2=4(cm),
∴BC=2BN=8(cm).
考点: 1.相似三角形的判定与性质;2.等腰三角形的性质;3.等边三角形的性质.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:填空题
已知点P是边长为4的正方形ABCD内一点,且PB="3" , BF⊥BP,垂足是点B, 若在射线BF上找一点M,使以点B, M, C为顶点的三角形与△ABP相似,则BM为___________.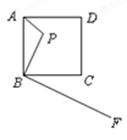
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
如图,将两块全等的直角三角形纸片△ABC和△DEF叠放在一起,其中∠ACB=∠E=90°,BC=DE=6,AC=FE=8,如图,将△DEF绕点D旋转,点D与AB的中点重合,DE,DF分别交AC于点M,N,使DM=MN则重叠部分(△DMN)的面积为 
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
在直角三角形ABC中, ,
, 是斜边AB的中点,过
是斜边AB的中点,过 作
作 于
于 ,连结
,连结 交
交 于
于 ;过
;过 作
作 于
于 ,连结
,连结 交
交 于
于 ;过
;过 作
作 于
于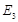 ,…,如此继续,可以依次得到点
,…,如此继续,可以依次得到点 ,
,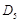 …,
…, ,分别记
,分别记 ,
, ,
, ,…,
,…, 的面积为
的面积为 ,
, ,
, ,…
,… ,则
,则 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com