
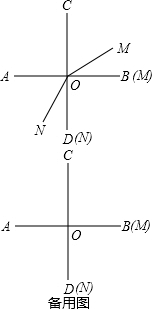
 如图,两条直线AB、CD相交于点O,且∠AOC=∠AOD,射线OM(与射线OB重合)绕O点逆时针方向旋转,速度为15°/s,射线ON(与射线OD重合)绕O点顺时针方向旋转,速度为12°/s.两射线OM、ON同时运动,运动时间为t秒.(本题出现的角均指小于平角的角)
如图,两条直线AB、CD相交于点O,且∠AOC=∠AOD,射线OM(与射线OB重合)绕O点逆时针方向旋转,速度为15°/s,射线ON(与射线OD重合)绕O点顺时针方向旋转,速度为12°/s.两射线OM、ON同时运动,运动时间为t秒.(本题出现的角均指小于平角的角)分析 (1)根据两条直线AB,CD相交于点O,∠AOC=∠AOD,可得图中一定有4个直角;当t=2时,根据射线OM,ON的位置,可得∠MON的度数,∠BON的度数以及∠MOC的度数;
(2)分两种情况进行讨论:当0<t≤7.5时,当7.5<t<12时,分别根据∠AOM=3∠AON-60°,列出方程式进行求解,即可得到t的值;
(3)先判断当∠MON为平角时t的值,再以此分两种情况讨论:当0<t<$\frac{10}{3}$时,当$\frac{10}{3}$<t<6时,分别计算$\frac{7∠COM+2∠BON}{∠MON}$的值,根据结果作出判断即可.
解答 解:(1)如图所示,∵两条直线AB,CD相交于点O,∠AOC=∠AOD,
∴∠AOC=∠AOD=90°,
∴∠BOC=∠BOD=90°,
∴图中一定有4个直角;
当t=2时,∠BOM=30°,∠NON=24°,
∴∠MON=30°+90°+24°=144°,∠BON=90°+24°=114°,∠MOC=90°-30°=60°;
故答案为:4;144°,114°,60°;
(2)当ON与OA重合时,t=90÷12=7.5(s),
当OM与OA重合时,t=180°÷15=12(s),
如图所示,当0<t≤7.5时,∠AON=90°-12t°,∠AOM=180°-15t°,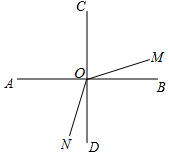
由∠AOM=3∠AON-60°,可得
180°-15t°=3(90°-12t°)-60°,
解得t=$\frac{10}{7}$;
如图所示,当7.5<t<12时,∠AON=12t°-90°,∠AOM=180°-15t°,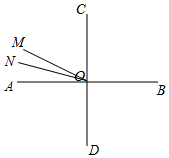
由∠AOM=3∠AON-60°,可得
180°-15t°=3(12t°-90°)-60°,
解得t=10;
综上所述,当∠AOM=3∠AON-60°时,t的值为$\frac{10}{7}$s或10s;
(3)当∠MON=180°时,∠BOM+∠BOD+∠DON=180°,
∴15t°+90°+12t°=180°,
解得t=$\frac{10}{3}$,
①如图所示,当0<t<$\frac{10}{3}$时,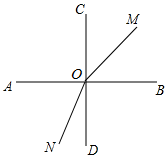
∠COM=90°-15t°,∠BON=90°+12t°,
∠MON=∠BOM+∠BOD+∠DON=15t°+90°+12t°,
∴$\frac{7∠COM+2∠BON}{∠MON}$=$\frac{7(90°-15t°)+2(90°+12t°)}{15t°+90°+12t°}$=$\frac{810°-81t°}{27t+90°}$(不是定值),
②如图所示,当$\frac{10}{3}$<t<6时,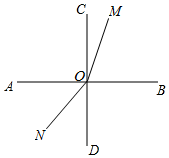
∠COM=90°-15t°,∠BON=90°+12t°,
∠MON=360°-(∠BOM+∠BOD+∠DON)=360°-(15t°+90°+12t°)=270°-27t°,
∴$\frac{7∠COM+2∠BON}{∠MON}$=$\frac{7(90°-15t°)+2(90°+12t°)}{270°-27t°}$=$\frac{810°-81t°}{270°-27t°}$=3(定值),
综上所述,当0<t<$\frac{10}{3}$时,$\frac{7∠COM+2∠BON}{∠MON}$的值不是定值,当$\frac{10}{3}$<t<6时,$\frac{7∠COM+2∠BON}{∠MON}$的值是3.
点评 本题属于角的计算综合题,主要考查了角的和差关系的运用,解决问题的关键是将相关的角用含t的代数式表示出来,并根据题意列出方程进行求解,以及进行分类讨论,解题时注意方程思想和分类思想的灵活运用.


科目:初中数学 来源: 题型:选择题
| A. | a-b+c=a+(b-c) | B. | a-b+c=a+(b+c) | C. | a-b+c=a-(b+c) | D. | a-b+c=a-(b-c) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (5,1) | B. | (-3,2) | C. | (-1,5) | D. | (3,-2) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
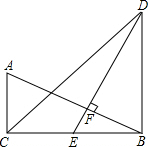 如图,在△ABC和△DBC中,∠ACB=∠DBC=90°,E是BC的中点,DE⊥AB,垂足为点F,且AB=DE.
如图,在△ABC和△DBC中,∠ACB=∠DBC=90°,E是BC的中点,DE⊥AB,垂足为点F,且AB=DE.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
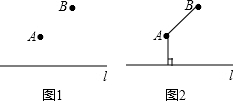 在数学课上,老师提出如下问题:
在数学课上,老师提出如下问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com