
(1)x2-3xy+2y2
分析:把x2-3xy+2y2看成关于x的二次三项式,这时,常数项是2y2,一次项系数是 -3y.把2y2分解成-y与-2y的积,(-y)+(-2y)=-3y,正好等于一次项系数.
解:(1)x2-3xy+2y2=x2-3yx+2y2=(x-y)(x-2y).
(2)a2+10ab-24b2;
(3)-5(x+y)z+(x+y)2-14z2;
(4)y4-(a2+b2)y2+a2b2.
科目:初中数学 来源: 题型:
| 3 |
| 2 |
| 3 |
| 3 |
| 2 |
| 3 |
| 3 |
| 2 |
| 3 |
| 3 |
| 2 |
| 3 |
| 3 |
| 3 |
|
| 2 |
| 3 |
| 13 |
| 6 |
| 2 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
|
|
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源:101网校同步练习 初二数学 华东师大(新课标2001-3年初审) 华东师大(新课标2001-3年初审) 题型:044
先阅读第(1)题的解法,再解答其它各题
(1)已知y=![]() +2007,求
+2007,求![]() 的值;
的值;
解:(1)由![]() 得x=2008,∴y=2007,∴
得x=2008,∴y=2007,∴![]() .
.
(2)若x、y为实数,且y>![]() +2008,化简
+2008,化简![]() ;
;
(3)如果![]() =0,求
=0,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
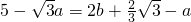 ,求a,b的值.
,求a,b的值.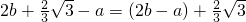 ,而
,而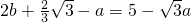 .
.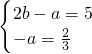 ,故
,故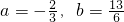 .
. ,求x,y的值.
,求x,y的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
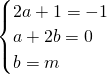 ,解得
,解得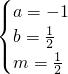 ,∴
,∴
 ,
,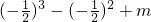 =0,故
=0,故  .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com