
【题目】(1)观察猜想
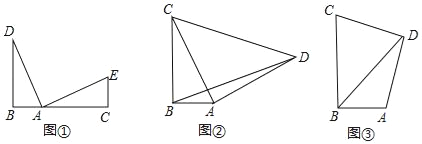
如图①点B、A、C在同一条直线上,DB⊥BC,EC⊥BC且∠DAE=90°,AD=AE,则BC、BD、CE之间的数量关系为;
(2)问题解决
如图②,在Rt△ABC中,∠ABC=90°,CB=4,AB=2,以AC为直角边向外作等腰Rt△DAC,连结BD,求BD的长;
(3)拓展延伸
如图③,在四边形ABCD中,∠ABC=∠ADC=90°,CB=4,AB=2,DC=DA,请直接写出BD的长.
【答案】(1)BC=BD+CE,(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)证明△ADB≌△EAC,根据全等三角形的性质得到BD=AC,EC=AB,即可得到BC、BD、CE之间的数量关系;
(2)过D作DE⊥AB,交BA的延长线于E,证明△ABC≌△DEA,得到DE=AB=2,AE=BC=4,Rt△BDE中,BE=6,根据勾股定理即可得到BD的长;
(3)过D作DE⊥BC于E,作DF⊥AB于F,证明△CED≌△AFD,根据全等三角形的性质得到CE=AF,ED=DF,设AF=x,DF=y,根据CB=4,AB=2,列出方程组,求出
![]() 的值,根据勾股定理即可求出BD的长.
的值,根据勾股定理即可求出BD的长.
解:(1)观察猜想
结论: BC=BD+CE,理由是:
如图①,∵∠B=90°,∠DAE=90°,
∴∠D+∠DAB=∠DAB+∠EAC=90°,
∴∠D=∠EAC,
∵∠B=∠C=90°,AD=AE,
∴△ADB≌△EAC,
∴BD=AC,EC=AB,
∴BC=AB+AC=BD+CE;
(2)问题解决
如图②,过D作DE⊥AB,交BA的延长线于E,
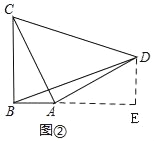
由(1)同理得:△ABC≌△DEA,
∴DE=AB=2,AE=BC=4,
Rt△BDE中,BE=6,
由勾股定理得: ![]()
(3)拓展延伸
如图③,过D作DE⊥BC于E,作DF⊥AB于F,
同理得:△CED≌△AFD,
∴CE=AF,ED=DF,
设AF=x,DF=y,
则![]() ,解得:
,解得:![]()
∴BF=2+1=3,DF=3,
由勾股定理得:![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】下列一组方程:①![]() ,②
,②![]() ,③
,③![]() ,…小明通过观察,发现了其中蕴含的规律,并顺利地求出了前三个方程的解第①个方程的解为
,…小明通过观察,发现了其中蕴含的规律,并顺利地求出了前三个方程的解第①个方程的解为![]() ;第②个方程的解为
;第②个方程的解为![]() ;第③个方程的解为
;第③个方程的解为![]() .若n为正整数,且关于x的方程
.若n为正整数,且关于x的方程![]() 的一个解是
的一个解是![]() ,则n的值等于____________.
,则n的值等于____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC.以AB为直径的⊙O分别与BC、AC相交于点D、E,连接AD.过点D作DF⊥AC,垂足为点F,
(1)求证:DF是⊙O的切线;
(2)若⊙O的半径为4,∠CDF=22.5°,求图中阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,为了改造小区环境,某小区决定要在一块一边靠墙(墙的最大可使用长度12m)的空地上建造一个矩形绿化带.除靠墙一边(AD)外,用长为32m的栅栏围成矩形ABCD.设绿化带宽AB为xm,面积为Sm2,
(1)求S与x的函数关系式,并直接写出x的取值范围;
(2)绿化带的面积能达到128m2吗?若能,请求出AB的长度;若不能,请说明理由;
(3)当x为何值时,满足条件的绿化带面积最大.

查看答案和解析>>
科目:初中数学 来源: 题型:
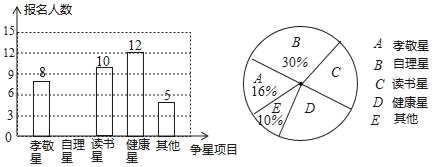
【题目】某小学开展寒假争星活动,学生可以从“自理星”、“读书星”、“健康星”、“孝敬星”等中选一个项目参加争星竞选,根据该校一年级某班学生的“争星”报名情况,绘制成了如下两幅不完整的统计图,请根据图中信息回答下列问题:
(1)参加调查的学生共有 人.
(2)将条形统计图补充完整;
(3)请计算扇形统计图中“读书星”对应的扇形圆心角度数;
(4)根据调查结果,试估计该小学全校3600名学生中争当“健康星”的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与y轴交于点C,与反比例函数y=![]() 的图象交于A,B两点,过点B作BE⊥x轴于点E,已知A点坐标是(2,4),BE=2.
的图象交于A,B两点,过点B作BE⊥x轴于点E,已知A点坐标是(2,4),BE=2.
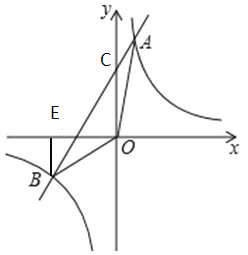
(1)求一次函数与反比例函数的表达式;
(2)连接OA、OB,求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在水平地面点A处有一网球发射器向空中发射网球,网球飞行路线是一条抛物线,在地面上落点为B,有人在直线AB上点C(靠点B一侧)竖直向上摆放若干个无盖的圆柱形桶.试图让网球落入桶内,已知AB=4米,AC=3米,网球飞行最大高度OM=5米,圆柱形桶的直径为0.5米,高为0.3米(网球的体积和圆柱形桶的厚度忽略不计).当竖直摆放圆柱形桶至少( )个时,网球可以落入桶内.

A.7B.8C.9D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
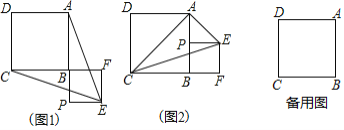
【题目】已知正方形ABCD,P为射线AB上的一点,以BP为边作正方形BPEF,使点F在线段CB的延长线上,连接EA、EC.
(1)如图1,若点P在线段AB的延长线上,求证:EA=EC;
(2)若点P在线段AB上,如图2,当点P为AB的中点时,判断△ACE的形状,并说明理由;
(3)在(1)的条件下,将正方形ABCD固定,正方形BPEF绕点B旋转一周,设AB=4,BP=a,若在旋转过程中△ACE面积的最小值为4,请直接写出a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
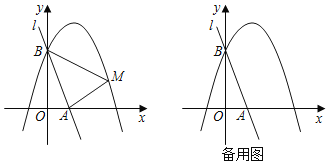
【题目】如图,直线l:y=﹣3x+3与x轴、y轴分别相交于A、B两点,抛物线y=ax2﹣2ax+a+4(a<0)经过点B.
(1)求该抛物线的函数表达式;
(2)已知点M是抛物线上的一个动点,并且点M在第一象限内,连接AM、BM,设点M的横坐标为m,△ABM的面积为S,求S与m的函数表达式,并求出S的最大值;
(3)在(2)的条件下,当S取得最大值时,动点M相应的位置记为点M′.写出点M′的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com