
【题目】如图,直线y=kx+2与x轴、y轴分别交于A、B两点,OA:OB=![]() .以线段AB为边在第二象限内作等腰Rt△ABC,∠BAC=90°.
.以线段AB为边在第二象限内作等腰Rt△ABC,∠BAC=90°.
(1)求点A的坐标和k的值;
(2)求点C坐标;
(3)直线y=![]() x在第一象限内的图象上是否存在点P,使得△ABP的面积与△ABC的面积相等?如果存在,求出点P坐标;如果不存在,请说明理由.
x在第一象限内的图象上是否存在点P,使得△ABP的面积与△ABC的面积相等?如果存在,求出点P坐标;如果不存在,请说明理由.
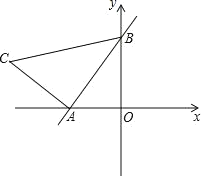
【答案】(1)A(﹣1,0),k=2;(2)C(﹣3,1);(3)P坐标为(2,1).
【解析】
(1)对于直线y=kx+2,令x=0求出y的值,确定出B坐标,得到OB的长,根据OA与OB比值求出OA的长,确定出A坐标,代入直线方程即可求出k的值;
(2)过C作CM垂直于x轴,利用同角的余角相等得到一对角相等,再由一对直角相等,以及AC=AB,利用AAS得到三角形ACM与三角形BAO全等,由全等三角形对应边相等得到CM=OA,AM=OB,由AM+OA求出OM的长,即可确定出C坐标;
(3)假设存在点P使得△ABP的面积与△ABC的面积相等,在直线y= ![]() x第一象限上取一点P,连接BP,AP,设点P(m,
x第一象限上取一点P,连接BP,AP,设点P(m,![]() m),由三角形ABO面积+三角形BPO面积-三角形AOP面积表示出三角形ABP面积,求出三角形AOB面积,两者相等求出m的值,即可确定出P坐标.
m),由三角形ABO面积+三角形BPO面积-三角形AOP面积表示出三角形ABP面积,求出三角形AOB面积,两者相等求出m的值,即可确定出P坐标.
(1)对于直线y=kx+2,令x=0,得到y=2,即B(0,2),OB=2,
∵OA:OB=![]() ,∴OA=1,即A(﹣1,0),
,∴OA=1,即A(﹣1,0),
将x=﹣1,y=0代入直线解析式得:0=﹣k+2,即k=2;
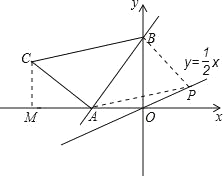
(2)过C作CM⊥x轴,可得∠AMC=∠BOA=90°,
∴∠ACM+∠CAM=90°,
∵△ABC为等腰直角三角形,即∠BAC=90°,AC=BA,
∴∠CAM+∠BAO=90°,
∴∠ACM=∠BAO,
在△CAM和△ABO中,
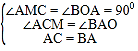 ,
,
∴△CAM≌△ABO(AAS),
∴AM=OB=2,CM=OA=1,即OM=OA+AM=1+2=3,
∴C(﹣3,1);
(3)假设存在点P使得△ABP的面积与△ABC的面积相等,在直线y=![]() x第一象限上取一点P,连接BP,AP,
x第一象限上取一点P,连接BP,AP,
设点P(m,![]() m),
m),
∴S△ABP=S△ABO+S△BPO﹣S△AOP=1+m﹣![]() m=1+
m=1+![]() m,而S△ABC=
m,而S△ABC=![]() ABAC=
ABAC=![]() AB2=
AB2=![]() (12+22)=
(12+22)=![]() ,
,
可得1+![]() m=
m=![]() ,
,
解得:m=2,
则P坐标为(2,1).


科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,∠B=30°,分别以点A和点B为圆心,大于![]() AB的长为半径作弧,两弧相交于M、N两点,作直线MN,交BC于点D,连接AD.
AB的长为半径作弧,两弧相交于M、N两点,作直线MN,交BC于点D,连接AD.
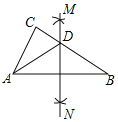
(1)根据作图判断:△ABD的形状是 ;
(2)若BD=10,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在 A 时测得某树(垂直于地面)的影长为 4 米,B 时又测得该树的影长为 16 米,若两次日 照的光线互相垂直,则树的高度为_____米.
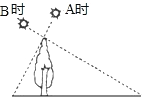
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人相约周末登花果山,甲、乙两人距地面的高度![]() (米)与登山时间
(米)与登山时间![]() (分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山上升的速度是每分钟 米,乙在![]() 地时距地面的高度
地时距地面的高度![]() 为 米;
为 米;
(2)若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,请求出乙登山全程中,距地面的高度![]() (米)与登山时间
(米)与登山时间![]() (分)之间的函数关系式.
(分)之间的函数关系式.
(3)登山多长时间时,甲、乙两人距地面的高度差为50米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人相约周末登花果山,甲、乙两人距地面的高度![]() (米)与登山时间
(米)与登山时间![]() (分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山上升的速度是每分钟 米,乙在![]() 地时距地面的高度
地时距地面的高度![]() 为 米;
为 米;
(2)若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,请求出乙登山全程中,距地面的高度![]() (米)与登山时间
(米)与登山时间![]() (分)之间的函数关系式.
(分)之间的函数关系式.
(3)登山多长时间时,甲、乙两人距地面的高度差为50米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为保障北京2022 年冬季奥运会赛场间的交通服务,北京将建设连接北京城区-延庆区-崇礼县三地的高速铁路和高速公路.在高速公路方面,目前主要的交通方式是通过京藏高速公路(G6),其路程为220公里.为将崇礼县纳入北京一小时交通圈,有望新建一条高速公路,将北京城区到崇礼的道路长度缩短到100公里.如果行驶的平均速度每小时比原来快22公里,那么从新建高速行驶全程所需时间与从原高速行驶全程所需时间比为4:11.求从新建高速公路行驶全程需要多少小时?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】酒泉市教育局计划对全市八年级学生学习情况进行调查,随机从全市抽取城市和农村两组学生的期中数学成绩,每组10人进行对比分析.绘制统计图如下.根据图中信息,完成下列问题.
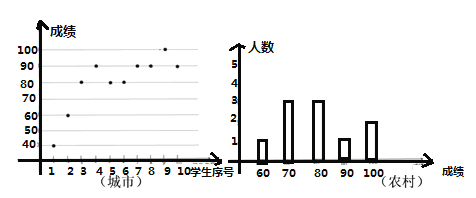
(1)完成下表;
平均数 | 中位数 | 众数 | 方差 | |
城市 | ||||
农村 |
(2)依据上表的信息谈谈你的看法.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦AD平分∠BAC,DE⊥AC交AC的延长线于点E.
(1)求证:DE是⊙O的切线;
(2)若AD=BC,⊙O半径为6,求∠CAD与![]() 围成的阴影部分的面积.
围成的阴影部分的面积.
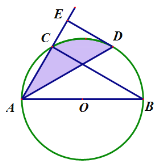
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市某楼盘准备以每平方米6000元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望,为了加快资金周转,房地产开发商对价格经过两次下调后,决定以每平方米4860元的均价开盘销售.
(1)求平均每次下调的百分率;
(2)某人准备以开盘均价购买一套100平方米的房子,开发商给予以下两种优惠方案供其选择:①打9.8折销售;②不打折,送两年物业管理费.物业管理费每平方米每月1.5元,请问哪种方案更优惠?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com