
【题目】如图,抛物线![]() 的顶点坐标为
的顶点坐标为![]() ,并且与
,并且与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于
轴交于![]() 、
、![]() 两点.
两点.
(![]() )求抛物线的表达式.
)求抛物线的表达式.
(![]() )如图
)如图![]() ,设抛物线的对称轴与直线
,设抛物线的对称轴与直线![]() 交于点
交于点![]() ,点
,点![]() 为直线
为直线![]() 上一动点,过点
上一动点,过点![]() 作
作![]() 轴的平行线
轴的平行线![]() ,与抛物线交于点
,与抛物线交于点![]() ,问是否存在点
,问是否存在点![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似.若存在,求出点
相似.若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() 或
或![]() 或
或![]() .
.
【解析】试题分析:(1)设抛物线的表达式为y=a(x-2)2-1(a≠0),将点C的坐标代入即可得出答案;(2)由直线BC的解析式知,∠OBC=∠OCB=45°.又由题意知∠EFD=∠COB=90°,所以只有△EFD∽△COB,根据这种情况求点E的坐标即可.
试题解析:
(![]() )该抛物线的顶点坐标为
)该抛物线的顶点坐标为![]() ,所以该抛物线的解析式为
,所以该抛物线的解析式为![]() ,又该抛物线过点
,又该抛物线过点![]() ,代入
,代入![]() 得:
得:
![]() ,解得
,解得![]() ,故该抛物线的解析式为
,故该抛物线的解析式为![]() +3.
+3.
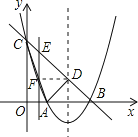
(![]() )假设存在点E,使得以D、E、F为顶点的三角形与△BCO相似.
)假设存在点E,使得以D、E、F为顶点的三角形与△BCO相似.
由(1)知,该抛物线的解析式是y=x2-4x+3,即y=(x-1)(x-3),
∴该抛物线与x轴的交点坐标分别是A(1,0),B(3,0).
∵C(0,3),
∴易求直线BC的解析式为:y=-x+3.
∴∠OBC=∠OCB=45°.
又∵点D是对称轴上的一点,
∴D(2,1).
如图,连接DF.
∵EF∥y轴,
∴只有∠EFD=∠COB=90°.
∵以D、E、F为顶点的三角形与△BCO相似,
∴∠DEF=∠FDE=45°,
∴只有△EFD∽△COB.
设E(x,-x+3),则F(x,1),
∴1=x2-4x+3,
解得x=2±![]() ,
,
当x=2+![]() 时,y=-x+3=1-
时,y=-x+3=1-![]() ;
;
当x=2-![]() 时,y=-x+3=1+
时,y=-x+3=1+![]() ;
;
∴E1(2-![]() ,1+
,1+![]() )、E2(2+
)、E2(2+![]() ,1-
,1-![]() ).
).
∠EDF=90°;易知,直线AD:y=x-1,联立抛物线的解析式有:
x2-4x+3=x-1,解得 x1=1、x2=4;
当x=1时,y=-x+3=2;
当x=4时,y=-x+3=-1;
∴E3(1,2)、E4(4,-1).
∴综上,点E的坐标为(2-![]() ,1+
,1+![]() )或(2+
)或(2+![]() ,1-
,1-![]() )或(1,2)或(4,-1).
)或(1,2)或(4,-1).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,BD为一条对角线,AD∥BC,AD=2BC,∠ABD=90°,E为AD的中点,连接BE.
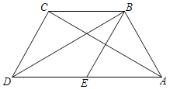
(1)求证:四边形BCDE为菱形;
(2)连接AC,若AC平分∠BAD,AB=2,求菱形BCDE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】银泰百货名创优品店购进600个钥匙扣,进价为每个8元,第一周以每个12元的价格售出200个,第二周若按每个12元的价格销售仍可售出200个,但商店为了适当增加销量,决定降价销售.据市场调查,单价每降低1元,可多售出50个,但售价不得低于进价,单价降低![]() 元销售,销售一周后,商店对剩余钥匙扣清仓处理,以每个6元的价格全部售出.
元销售,销售一周后,商店对剩余钥匙扣清仓处理,以每个6元的价格全部售出.
(1)如果这批钥匙扣共获利1050元,那么第二周每个钥匙扣的销售价格为多少元?
(2)这次降价活动,1050元是最高利润吗?若是,说明理由;若不是,求出最高利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家2015年的四个季度的用电量情况如表1,其中各种电器用电量情况如表2.
表1 | 表2 | |||
季度名称 | 用电量/度 | 电器 | 用电量/度 | |
第一季度 | 250 | 空调 | 250 | |
第二季度 | 150 | 冰箱 | 400 | |
第三季度 | 400 | 彩电 | 150 | |
第四季度 | 200 | 其他 | 100 | |
小明根据上面的数据制成如图所示的统计图.


根据以上三幅统计图回答下列问题:
(1)从哪幅统计图中可以看出各季度用电量变化情况?
(2)从哪幅统计图中可以看出冰箱的用电量超过总用电量的![]() ?
?
(3)从哪幅统计图中可以清楚地看出空调的用电量?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划购进![]() 、
、![]() 两种新型节能台灯共
两种新型节能台灯共![]() 盏,这两种台灯的进价、售价如表所示:
盏,这两种台灯的进价、售价如表所示:

(![]() )若商场预计进货款为
)若商场预计进货款为![]() 元,则这两种台灯各购进多少盏?
元,则这两种台灯各购进多少盏?
(![]() )若商场规定
)若商场规定![]() 型台灯的进货数量不超过
型台灯的进货数量不超过![]() 型台灯数量的
型台灯数量的![]() 倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?
倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
问题背景:
我们知道,三角形的中位线平行于三角形的第三边,并且等于第三边的一半,如何证明三角形中位线定理呢?
已知:如图1,在![]() 中,
中,![]() 分别是
分别是![]() 的中点.
的中点.

求证:![]()
问题中既要证明两条线段所在的直线平行,又要证明其中一条线段的长等于另一线段长的一半.所以可以用“倍长法”将![]() 延长一倍:延长
延长一倍:延长![]() 到
到![]() ,使得
,使得![]() ,连接
,连接![]() 这样只需证明
这样只需证明![]() ,且
,且![]() .由于
.由于![]() 是
是![]() 的中点,容易证明四边形
的中点,容易证明四边形![]() 、四边形
、四边形![]() 是平行四边形,证明...
是平行四边形,证明...
问题解决:
![]() 上述材料中“倍长法”体现的数学思想主要是_____. (填入选项前的字母代号即可)
上述材料中“倍长法”体现的数学思想主要是_____. (填入选项前的字母代号即可)
A.数形结合思想 B.转化思想 C.分类讨论思想 D.方程思想
![]() 证明四边形
证明四边形![]() 是平行四边形的依据是
是平行四边形的依据是

反思交流:
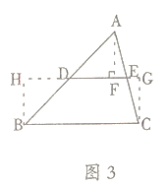
“智慧小组”在证明中位线定理时,在图1的基础上追加了如上辅助线作法:如图3,分别过点![]() 作
作![]() 的垂线,垂足分别为
的垂线,垂足分别为![]() ,..
,..
![]() 请你根据“智慧小组”添加的辅助线,证明三角形的中位线定理.
请你根据“智慧小组”添加的辅助线,证明三角形的中位线定理.
方法迁移:
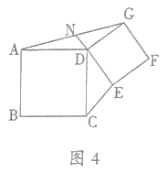
![]() 如图4、四边形
如图4、四边形![]() 和
和![]() 都是正方形,
都是正方形,![]() 是
是![]() 的中点.求证:
的中点.求证: ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格中进行下列操作:

(1)请在图中确定该圆弧所在圆心D点的位置,D点坐标为 ;
(2)连接AD、CD,求⊙D的半径及扇形DAC的圆心角度数;
(3)若扇形DAC是某一个圆锥的侧面展开图,求该圆锥的底面半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在Rt△ABC中,∠ACB=90°,∠A=30°,AB=4,点D在直线BC上,E在AC上,且AC=CD,DE=AB.
(1)如图②,将△ECD沿CB方向平移,使点E落在AB上,得△E1C1D1,求平移的距离;
(2)如图③,将△ECD绕点C逆时针旋转,使点E落在AB上,得△E2CD2,求旋转角∠DCD2的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com