Question

1．问题提出：有同样大小正方形256个，拼成如图1所示的16×16的一个大的正方形．请问如果用一条直线穿过这个大正方形的话，最多可以穿过多少个小正方形？

我们先考虑以下简单的情况：一条直线穿越一个正方形的情况．（如图2）
从图2中我们可以看出，当一条直线穿过一个小正方形时，这条直线最多与正方形上、下、左、右四条边中的两个边相交，所以当一条直线穿过一个小正方形时，这条直线会与其中某两条边产生两个交点，并且以两个交点为顶点的线段会全部落在小正方形内．
这就启发我们：为了求出直线L最多穿过多少个小正方形，我们可以转而去考虑当直线L穿越由小正方形拼成的大正方形时最多会产生多少个交点．然后由交点数去确定有多少根小线段，进而通过线段的根数确定下正方形的个数．
再让我们来考虑3×3正方形的情况（如图3）：为了让直线穿越更多的小正方形，我们不妨假设直线L右上方至左下方穿过一个3×3的正方形，我们从两个方向来分析直线l穿过3×3正方形的情况：从上下来看，这条直线由下至上最多可穿过上下平行的两条线段；从左右来看，这条直线最多可穿过左右平行的四条线段；这样直线L最多可穿过3×3的大正方形中的六条线段，从而直线L上会产生6个交点，这6个交点之间的5条线段，每条会落在一个不同的正方形内，因此直线L最多能经过5个小正方形．
问题解决：
（1）有同样大小的小正方形16个，拼成如图4所示的4×4的一个大的正方形．请问如果用一条直线穿过这个大正方形的话，最多可以穿过7个小正方形？
（2）有同样大小的小正方形100个，拼成10×10的一个大的正方形．请问如果用一条直线穿过这个大正方形的话，最多可以穿过19个小正方形？
（3）有同样大小的小正方形256个，拼成16×16的一个大的正方形．请问如果用一条直线穿过这个大正方形的话，最多可以穿过31个小正方形？
（4）请问如果用一条直线穿n×n大正方形的话，最多可以穿过2n-1个小正方形？
拓展探究：
（5）请问如果用一条直线穿2×3大长方形的话（如图5），最多可以穿过4个小正方形？
（6）请问如果用一条直线穿3×4大长方形的话（如图6），最多可以穿过6个小正方形？
（7）请问如果用一条直线穿m×n大长方形的话，最多可以穿过m+n-1个小正方形？
请将你的推理过程进行简要的叙述．
类比探究：由二维的平面我们可以联想到三维的立体空间，平面中的正方形中四条边可联想到正方体中的正方形的六个面，类比上面问题解决的方法解决如下问题．
（8）如图①有同样大小的小正方体8个，拼成如图①所示的2×2×2的一个大的正方体．请问如果用一条直线穿过这个大正方体的话，最多可以穿过多少个小正方体？

（9）请问如果用一条直线穿过n×n×n大正方体的话，最多可以穿过多少个小正方体？

Answer 1

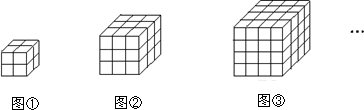
分析 （1）为了让直线穿越更多的小正方形，我们不妨假设直线L右上方至左下方穿过一个4×4的正方形，我们从两个方向来分析直线l穿过4×4正方形的情况：从上下来看，这条直线由下至上最多可穿过上下平行的3条线段；从左右来看，这条直线最多可穿过左右平行的5条线段；这样直线L最多可穿过4×4的大正方形中的8条线段，从而直线L上会产生8个交点，这8个交点之间的7条线段，这样就不难得到答案．
（2）应用规律2n-1得到答案．
（3）应用规律2n-1得到答案．
（4）应用规律2n-1得到答案．
（5）我们不妨假设直线L右上方至左下方穿过一个2×3的正方形，我们从两个方向来分析直线l穿过2×3正方形的情况：从上下来看，这条直线由下至上最多可穿过上下平行的1条线段；从左右来看，这条直线最多可穿过左右平行的4条线段；这样直线L最多可穿过2×3的大正方形中的5条线段，从而直线L上会产生5个交点，这5个交点之间的4条线段，每条会落在一个不同的正方形内，因此直线L最多能经过4个小正方形．
（6）不妨假设直线L右上方至左下方穿过一个3×4的正方形，我们从两个方向来分析直线l穿过3×4正方形的情况：从上下来看，这条直线由下至上最多可穿过上下平行的2条线段；从左右来看，这条直线最多可穿过左右平行的5条线段；这样直线L最多可穿过4×4的大正方形中的7条线段，从而直线L上会产生7个交点，这7个交点之间的6条线段，每条会落在一个不同的正方形内，因此直线L最多能经过6个小正方形．
（7）不妨假设直线L右上方至左下方穿过一个m×n的正方形，我们从两个方向来分析直线l穿过m×n正方形的情况：从上下来看，这条直线由下至上最多可穿过上下平行的（m-1）条线段；从左右来看，这条直线最多可穿过左右平行的（n+1）条线段；这样直线L最多可穿过4×4的大正方形中的（m+n）条线段，从而直线L上会产生（m+n）个交点，这m+n个交点之间的（m+n-1）条线段，每条会落在一个不同的正方形内，因此直线L最多能经过（m+n-1）个小正方形．
（8）用类似的方法得到规律：3n-2．即可解决．
（9）根据规律3n-2得到答案．

解答 解：（1）再让我们来考虑4×4正方形的情况（如图4）：为了让直线穿越更多的小正方形，我们不妨假设直线L右上方至左下方穿过一个4×4的正方形，我们从两个方向来分析直线l穿过4×4正方形的情况：从上下来看，这条直线由下至上最多可穿过上下平行的3条线段；从左右来看，这条直线最多可穿过左右平行的5条线段；这样直线L最多可穿过4×4的大正方形中的8条线段，从而直线L上会产生8个交点，这8个交点之间的7条线段，每条会落在一个不同的正方形内，因此直线L最多能经过7个小正方形．
故答案为7
（2）我们发现直线穿越1×1正方形时最多经过1个正方形，直线穿越2×2正方形时最多经过3个正方形，直线穿越3×3正方形时最多经过5个正方形，
直线穿越4×4正方形时最多经过7个正方形，…直线穿越n×n正方形时最多经过2n-1个正方形．
∴直线穿越10×10正方形时最多经过19个正方形．
故答案为19．
（3）由（2）可知，有2×16-1=31个正方形，
故答案为31．
（4）由（2）可知有2n-1个正方形．
故答案为2n-1．
（5）为了让直线穿越更多的小正方形，我们不妨假设直线L右上方至左下方穿过一个2×3的正方形，我们从两个方向来分析直线l穿过2×3正方形的情况：从上下来看，这条直线由下至上最多可穿过上下平行的1条线段；从左右来看，这条直线最多可穿过左右平行的4条线段；这样直线L最多可穿过2×3的大正方形中的5条线段，从而直线L上会产生5个交点，这5个交点之间的4条线段，每条会落在一个不同的正方形内，因此直线L最多能经过4个小正方形，
故答案为4．
（6）为了让直线穿越更多的小正方形，我们不妨假设直线L右上方至左下方穿过一个3×4的正方形，我们从两个方向来分析直线l穿过3×4正方形的情况：从上下来看，这条直线由下至上最多可穿过上下平行的2条线段；从左右来看，这条直线最多可穿过左右平行的5条线段；这样直线L最多可穿过4×4的大正方形中的7条线段，从而直线L上会产生7个交点，这7个交点之间的6条线段，每条会落在一个不同的正方形内，因此直线L最多能经过6个小正方形．
故答案为6．
（7）为了让直线穿越更多的小正方形，我们不妨假设直线L右上方至左下方穿过一个m×n的正方形，我们从两个方向来分析直线l穿过m×n正方形的情况：从上下来看，这条直线由下至上最多可穿过上下平行的（m-1）条线段；从左右来看，这条直线最多可穿过左右平行的（n+1）条线段；这样直线L最多可穿过4×4的大正方形中的（m+n）条线段，从而直线L上会产生（m+n）个交点，这m+n个交点之间的（m+n-1）条线段，每条会落在一个不同的正方形内，因此直线L最多能经过（m+n-1）个小正方形，
故答案为（m+n-1）．
（8）用类似的方法可以得到：用一条直线穿过1×1×1正方体的话，最多可以穿过1个小正方体，用一条直线穿过，2×2×2正方体的话，最多可以穿过4个小正方体，用一条直线穿过，3×3×3正方体的话，最多可以穿过7个小正方体，用一条直线穿过4×4×4正方体的话，最多可以穿过10个小正方体，…用一条直线穿过，n×n×n正方体的话，最多可以穿过（3n-2）个小正方体．
故答案为4．
（9）由（8）可知有（3n-2）个正方形，
故答案为（3n-2）．

点评 本题考查线线相交得点、以及正方形、立方体的有关知识，是个探究题目，学会从简单到复杂的推理方法，找到规律即可解决问题，本题难度比较大，从穿过的线段入手，找到问题的突破口，这个方法值得在以后的学习中应用．