
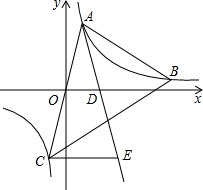
 如图,在平面直角坐标系xOy中,点A($\frac{1}{2}$,2),B(3,n),在反比例函数y=$\frac{m}{x}$(m为常数)的图象上,连接AO并延长与图象的另一支有另一个交点为点C,过点A的直线l与x轴的交点为点D(1,0),过点C作CE∥x轴交直线l于点E.
如图,在平面直角坐标系xOy中,点A($\frac{1}{2}$,2),B(3,n),在反比例函数y=$\frac{m}{x}$(m为常数)的图象上,连接AO并延长与图象的另一支有另一个交点为点C,过点A的直线l与x轴的交点为点D(1,0),过点C作CE∥x轴交直线l于点E.分析 (1)将点A($\frac{1}{2}$,2)代入y=$\frac{m}{x}$求出m的值,再将A($\frac{1}{2}$,2),D(1,0)分别代入y=kx+b,求出k、b的值;
(2)由反比例函数图象的中心对称性可知点C的坐标为C(-$\frac{1}{2}$,-2),由yE=yC求出E点坐标.
(3)作AF⊥BN于点G,与射线BN交于点G,作CH⊥BN 于点H,由于点B(3,n)在反比例函数图象上,求出n=$\frac{1}{3}$,在Rt△ABG中、Rt△BCH中,求出tan∠ABH和tan∠CBH的值即可.
解答 解:(1)∵点A($\frac{1}{2}$,2)在反比例函数y=$\frac{m}{x}$(m为常数)的图象上,
∴m=$\frac{1}{2}$×2=1.
∴反比例函数y=$\frac{m}{x}$(m为常数)对应的函数表达式是y=$\frac{1}{x}$.
设直线l对应的函数表达式为y=kx+b(k,b为常数,k≠0).
∵直线l经过点A($\frac{1}{2}$,2),D(1,0),
∴$\left\{\begin{array}{l}\frac{1}{2}k+b=2\\ k+b=0\end{array}\right.$,
解得$\left\{\begin{array}{l}k=-4\\ b=4\end{array}\right.$,
∴直线l对应的函数表达式为y=-4x+4.
(2)由反比例函数图象的中心对称性可知点C的坐标为C(-$\frac{1}{2}$,-2).
∵CE∥x轴交直线l于点E,
∴yE=yC.
∴点E的坐标为E($\frac{3}{2}$,-2).
(3)如图,作AF⊥BN于点G,与射线BN交于点G,作CH⊥BN 于点H,
∵点B(3,n)在反比例函数图象上,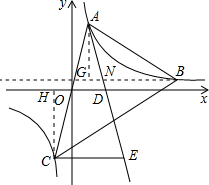
∴n=$\frac{1}{3}$,
∴B(3,$\frac{1}{3}$),G($\frac{1}{2}$,$\frac{1}{3}$),H(-$\frac{1}{2}$,$\frac{1}{3}$).
在Rt△ABG中,tan∠ABH=$\frac{AG}{BG}$=$\frac{2-\frac{1}{3}}{3-\frac{1}{2}}$=$\frac{2}{3}$,
在Rt△BCH中,tan∠CBH=$\frac{CH}{BH}$=$\frac{\frac{1}{3}+2}{3+\frac{1}{2}}$=$\frac{2}{3}$,
∴tan∠ABN=tan∠CBN.
点评 本题考查了反比例函数综合题,涉及待定系数法求函数解析式、反比例函数的性质、三角函数的定义等知识,值得关注.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 如图,一次函数y=kx+b的图象经过点A(6,0),点B(2,2),且与y轴相交于点C.请根据以上信息(不再添加其他条件),提出一个问题并尝试解答.你提出的问题是点C的坐标是什么;并请写出你的解答过程.
如图,一次函数y=kx+b的图象经过点A(6,0),点B(2,2),且与y轴相交于点C.请根据以上信息(不再添加其他条件),提出一个问题并尝试解答.你提出的问题是点C的坐标是什么;并请写出你的解答过程.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,D,E是BC的三等分点,BC=15cm,AD=13cm,AE=12cm,F,G分别是AB,AC的中点,求四边形DEGF的周长和面积.
如图,在△ABC中,D,E是BC的三等分点,BC=15cm,AD=13cm,AE=12cm,F,G分别是AB,AC的中点,求四边形DEGF的周长和面积.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在等腰梯形ABCD中,AD∥BC,AB=CD=3,P是BC上一点,PE∥CD交BD于点E,PF∥AB交AC于点F,设PE、PF的长分别是m、n,且x=m+n,那么当P在BC上移动时,x的值是否变化?若变化,求出x的取值范围;若不变,求出x的值.
如图,在等腰梯形ABCD中,AD∥BC,AB=CD=3,P是BC上一点,PE∥CD交BD于点E,PF∥AB交AC于点F,设PE、PF的长分别是m、n,且x=m+n,那么当P在BC上移动时,x的值是否变化?若变化,求出x的取值范围;若不变,求出x的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 初三某班对最近一次数学测验成绩(得分取整数) 进行统计分析,将所有成绩由低到高分成五组,并绘制成如下图所示的频数分布直方图,请结合直方图提供的 信息,回答下列问题:
初三某班对最近一次数学测验成绩(得分取整数) 进行统计分析,将所有成绩由低到高分成五组,并绘制成如下图所示的频数分布直方图,请结合直方图提供的 信息,回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com