Question

7．如图，AB是⊙O的直径，C，E，F为⊙O上的点，CA是∠BAF的平分线，过点C作CD⊥AF交AF的延长线于D点，CE⊥AB，垂足为点G．
（1）求证：DC是⊙O的切线；
（2）若sin∠BAC=$\frac{2}{5}$，求$\frac{{S}_{△CBE}}{{S}_{△ABC}}$的值（S表示面积）．

Answer 1

分析 （1）直接利用角平分线的性质结合等腰三角形的性质得出∠DAC=∠OCA，进而利用平行线的性质得出答案；
（2）利用锐角三角函数关系结合相似三角形的判定与性质表示出CG，AB的长，进而得出答案．

解答 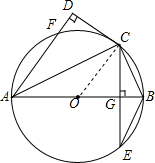（1）证明：连接CO，
∵CA是∠BAF的平分线，
∴∠DAC=∠CAB，
∵AO=CO，
∴∠OAC=∠OCA，
∴∠DAC=∠OCA，
∴AD∥CO，
∵CD⊥AF，
∴OC⊥DC，
∴DC是⊙O的切线；

（2）解：∵sin∠BAC=$\frac{2}{5}$，
∴$\frac{CG}{AC}$=$\frac{2}{5}$，
设GC=2x，AC=5x，
则AG=$\sqrt{21}$x，
∵∠BAC+∠ACG=90°，∠BCG+∠ACG=90°，
∴∠GAC=∠BCG，
又∵∠AGC=∠BGC，
∴△AGC∽△CGB，
∴$\frac{CG}{AG}$=$\frac{BG}{CG}$，
∴CG²=AG•BG，
故（2x）²=$\sqrt{21}$x•BG，
解得：BG=$\frac{4\sqrt{21}}{21}$x，
则AB=$\sqrt{21}$x+$\frac{4\sqrt{21}}{21}$x=$\frac{25\sqrt{21}}{21}$x，
故$\frac{{S}_{△CBE}}{{S}_{△ABC}}$=$\frac{{2S}_{△CBG}}{\frac{1}{2}CG•AB}$=$\frac{2×\frac{1}{2}×BG•GC}{\frac{1}{2}GC×AB}$=$\frac{\frac{4\sqrt{21}}{21}}{\frac{25\sqrt{21}}{21}}$=$\frac{4}{25}$．

点评 此题主要考查了切线的判定以及相似三角形的判定与性质等知识，正确表示出AB，BG的长是解题关键．