
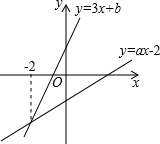
 如图,已知直线y=3x+b与y=ax-2的交点的横坐标为-2,则关于x的方程3x+b=ax-2的解为x=-2.
如图,已知直线y=3x+b与y=ax-2的交点的横坐标为-2,则关于x的方程3x+b=ax-2的解为x=-2.  特高级教师点拨系列答案
特高级教师点拨系列答案科目:初中数学 来源: 题型:解答题
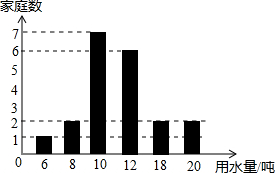 某校八年级去年12月份开展了家庭用水量调查活动,并约定:如果12月份的用水量在“选定标准”的±20%范围之内都称为“普通用水量”.现随机选出该年级20名学生,将其家庭12月份的用水量情况进行统计并绘制成如下统计图,请根据统计图信息解决问题:
某校八年级去年12月份开展了家庭用水量调查活动,并约定:如果12月份的用水量在“选定标准”的±20%范围之内都称为“普通用水量”.现随机选出该年级20名学生,将其家庭12月份的用水量情况进行统计并绘制成如下统计图,请根据统计图信息解决问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 一个反比例函数的图象如图所示,则该反比例函数的解析式为( )
一个反比例函数的图象如图所示,则该反比例函数的解析式为( )| A. | y=$\frac{3}{x}$ | B. | y=-$\frac{3}{x}$ | C. | y=$\frac{3}{x}({x>0})$ | D. | y=-$\frac{3}{x}({x>0})$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
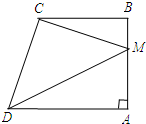 如图,四边形ABCD中,AD∥BC,∠BAD=90°,点M为AB上一点,连结CM,DM.
如图,四边形ABCD中,AD∥BC,∠BAD=90°,点M为AB上一点,连结CM,DM.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图所示,圆圈内分别标有1,2,…,12,这12个数字,电子跳蚤每跳一步,可以从一个圆圈逆时针跳到相邻的圆圈,若电子跳蚤所在圆圈的数字为n,则电子跳蚤连续跳(3n-2)步作为一次跳跃,例如:电子跳蚤从标有数字1的圆圈需跳3×1-2=1步到标有数字2的圆圈内,完成一次跳跃,第二次跳跃则要连续跳3×2-2=4步到达标有数字6的圆圈,….依此规律,若电子跳蚤从①开始,那么第3次能跳到的圆圈内所标的数字是10;第2014次电子跳蚤能跳到的圆圈内所标的数字为2.
如图所示,圆圈内分别标有1,2,…,12,这12个数字,电子跳蚤每跳一步,可以从一个圆圈逆时针跳到相邻的圆圈,若电子跳蚤所在圆圈的数字为n,则电子跳蚤连续跳(3n-2)步作为一次跳跃,例如:电子跳蚤从标有数字1的圆圈需跳3×1-2=1步到标有数字2的圆圈内,完成一次跳跃,第二次跳跃则要连续跳3×2-2=4步到达标有数字6的圆圈,….依此规律,若电子跳蚤从①开始,那么第3次能跳到的圆圈内所标的数字是10;第2014次电子跳蚤能跳到的圆圈内所标的数字为2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,△ABC中,AC=BC,CD⊥AB,垂足是D,点E是线段CD上一点,AE的延长线交BC于F.过B作AC的平行线交AE的延长线于G.
已知:如图,△ABC中,AC=BC,CD⊥AB,垂足是D,点E是线段CD上一点,AE的延长线交BC于F.过B作AC的平行线交AE的延长线于G.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com