
分析 (1)本题涉及乘方、绝对值、特殊角的三角函数值、二次根式化简四个考点.针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果;
(2)先求出不等式组的解集,然后在解集中求出非负整数即可.
解答 解:(1)22+|-1|-$\sqrt{4}$+(-2)2-$\sqrt{8}$+2sin45°+|-$\sqrt{2}$|
=4+1-2+4-2$\sqrt{2}$+2×$\frac{\sqrt{2}}{2}$+$\sqrt{2}$
=7;
(2)解不等式组$\left\{\begin{array}{l}{\frac{2}{3}x+5>1-x}\\{x-1<\frac{3}{4}x-\frac{1}{8}}\end{array}\right.$,得-$\frac{12}{5}$<x<$\frac{7}{2}$,
所以它的非负整数解为0,1,2,3.
点评 本题考查了(1)实数的综合运算能力,解题的关键是熟记特殊角的三角函数值,熟练掌握特殊角的三角函数值、乘方、二次根式、绝对值等考点的运算.
(2)一元一次不等式组的整数解,根据不等式的性质求出不等式组的解集是解题的关键.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
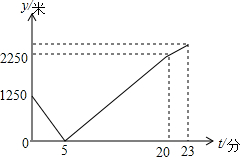 早晨,小刚沿着通往学校唯一的一条路(直路)上学,途中发现忘带饭盒,停下往家里打电话,妈妈接到电话后带上饭盒马上赶往学校,同时小刚返回,两人相遇后,小刚立即赶往学校,妈妈回家,15分钟妈妈到家,再经过3分钟小刚到达学校,小刚始终以100米/分的速度步行,小刚和妈妈的距离y(单位:米)与小刚打完电话后的步行时间t(单位:分)之间的函数关系如图,下列四种说法:
早晨,小刚沿着通往学校唯一的一条路(直路)上学,途中发现忘带饭盒,停下往家里打电话,妈妈接到电话后带上饭盒马上赶往学校,同时小刚返回,两人相遇后,小刚立即赶往学校,妈妈回家,15分钟妈妈到家,再经过3分钟小刚到达学校,小刚始终以100米/分的速度步行,小刚和妈妈的距离y(单位:米)与小刚打完电话后的步行时间t(单位:分)之间的函数关系如图,下列四种说法:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
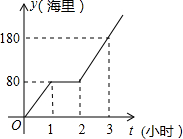 我国边防海警按照计划指定海域去巡逻,某巡逻艇匀速行驶一段时间后,因中途出现故障耽搁了一段时间,故障排除后,该艇加快速度仍匀速前进,结果恰好准点到达,如图是该艇行驶的路程y(海里)与所用时间t(小时)之间的函数图象,求该巡逻艇原计划准点到达指定海域所要行驶的路程.
我国边防海警按照计划指定海域去巡逻,某巡逻艇匀速行驶一段时间后,因中途出现故障耽搁了一段时间,故障排除后,该艇加快速度仍匀速前进,结果恰好准点到达,如图是该艇行驶的路程y(海里)与所用时间t(小时)之间的函数图象,求该巡逻艇原计划准点到达指定海域所要行驶的路程.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 宜兴市2010~2014年成年国民阅读调查报告的部分相关数据,绘制的统计图表如下:
宜兴市2010~2014年成年国民阅读调查报告的部分相关数据,绘制的统计图表如下:| 年份 | 年人均阅读图书数量(本) |
| 2010 | 3.90 |
| 2011 | 4.12 |
| 2012 | 4.35 |
| 2013 | 4.56 |
| 2014 | 4.78 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com