
【题目】《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.其中卷第九勾股,主要讲述了以测量问题为中心的直角三角形三边互求的关系.其中记载:“今有邑,东西七里,南北九里,各中开门,出东门一十五里有木,问:出南门几何步而见木?”
译文:“今有一座长方形小城,东西向城墙长7里,南北向城墙长9里,各城墙正中均开一城门.走出东门15里处有棵大树,问走出南门多少步恰好能望见这棵树?”(注:1里=300步)
你的计算结果是:出南门 步而见木.
 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】嘉淇准备完成题目:化简:![]() ,发现系数“
,发现系数“![]() ”印刷不清楚.
”印刷不清楚.
(1)他把“![]() ”猜成3,请你化简:(3x2+6x+8)–(6x+5x2+2);
”猜成3,请你化简:(3x2+6x+8)–(6x+5x2+2);
(2)他妈妈说:“你猜错了,我看到该题标准答案的结果是常数.”通过计算说明原题中“![]() ”是几?
”是几?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x、y的多项式(m﹣2)![]() +(n+3)xy2+3xy﹣5.
+(n+3)xy2+3xy﹣5.
(1)若原多项式是五次多项式,求m、n的值;
(2)若原多项式是五次四项式,求m、n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为加强电动自行车质量监管,切实保障消费者的合法权益,2015年11月,河南开封市工商局对24个品牌批次的电动自行车进行抽查检验,其中抽查检验的某品牌的电动自行车如图所示,它的大灯M射出的光线MA,MB的与MN的夹角分别为76°和60°,MN⊥地面CD,MN=0.8m,图中的阴影部分表示在夜晚时,灯M所照射的范围.(提示:![]() ≈1.7,sin14°
≈1.7,sin14°![]() , cos14°≈
, cos14°≈![]() , tan14
, tan14![]() )
)
(1)求阴影部分的面积;
(2)一般正常人从发现危险到做出刹车动作的反应时间是0.2s.小鹏某天晚上以6m/s的速度驾驶该车,在行驶的途中,通过大灯M,他发现在他的正前方有一个小球(即小孩在图中的点A处),小鹏从做出刹车动作到电动自行车停止的刹车距离为1.3m,请判断小鹏当时是否有撞到该小孩?(大灯M与前轮前端间的水平距离为0.3m).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明是个爱探究的学生,在学习完等腰三角形的判定定理之后,对于等腰![]() (如图甲),若
(如图甲),若![]() ,
,![]() ,小明发现,只要作
,小明发现,只要作![]() 的平分线就可以将
的平分线就可以将![]() 分成两个等腰三角形.
分成两个等腰三角形.
(1)你认为小明的发现正确吗?若正确,请给出证明过程;若不正确,请说明理由;
(2)请你对图乙的三角形进行探索,将![]() 分成两个等腰三角形,并写出顶角度数;
分成两个等腰三角形,并写出顶角度数;
(3)请你对图丙的三角形进行再探索,将![]() 分成三个等腰三角形,并写出顶角度数.
分成三个等腰三角形,并写出顶角度数.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠AOB=100°,∠COD=40°,OE平分∠AOC,OF平分∠BOD.(本题中的角均为大于0°且小于等于180°的角).
(1)如图1,当OB、OC重合时,求∠EOF的度数;
(2)当∠COD从图1所示位置绕点O顺时针旋转n°(0<n<90)时,∠AOE﹣∠BOF的值是否为定值?若是定值,求出∠AOE﹣∠BOF的值;若不是,请说明理由.
(3)当∠COD从图1所示位置绕点O顺时针旋转n°(0<n<180)时,满足∠AOD+∠EOF=6∠COD,则n=__________.
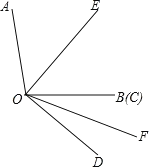
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将-2,-1,0,1,2,3,4,5,6,7这10个数分别填写在五角星中每两条线的交点处(每个交点处只填写一个数),将每一条线上的4个数相加,共得5个数,设为a1,a2,a3,a4,a5.
(1)求![]() (a1+a2+a3+a4+a5)的值;
(a1+a2+a3+a4+a5)的值;
(2)交换其中任何两位数的位置后,![]() (a1+a2+a3+a4+a5)的值是否改变?并说明理由.
(a1+a2+a3+a4+a5)的值是否改变?并说明理由.
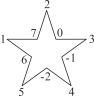
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我区某中学体育组因高中教学需要本学期购进篮球和排球共80个,共花费5800元,已知篮球的单价是80元/个,排球的单价是50元/个.
(1)篮球和排球各购进了多少个(列方程组解答)?
(2)因该中学秋季开学准备为初中也购买篮球和排球,教学资源实现共享,体育组提出还需购进同样的篮球和排球共40个,但学校要求花费不能超过2810元,那么篮球最多能购进多少个(列不等式解答)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2) 如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=![]() ,其中
,其中![]() 为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com