
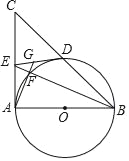
【题目】已知:如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,DE⊥AC于E.
(1)求证:DE为⊙O的切线;
(2)G是ED上一点,连接BE交圆于F,连接AF并延长交ED于G.若GE=2,AF=3,求EF的长.
【答案】(1)见解析;(2)∠EAF的度数为30°
【解析】
(1)连接OD,如图,先证明OD∥AC,再利用DE⊥AC得到OD⊥DE,然后根据切线的判定定理得到结论;
(2)利用圆周角定理得到∠AFB=90°,再证明Rt△GEF∽△Rt△GAE,利用相似比得到![]() 于是可求出GF=1,然后在Rt△AEG中利用正弦定义求出∠EAF的度数即可.
于是可求出GF=1,然后在Rt△AEG中利用正弦定义求出∠EAF的度数即可.
(1)证明:连接OD,如图,
∵OB=OD,
∴∠OBD=∠ODB,
∵AB=AC,
∴∠ABC=∠C,
∴∠ODB=∠C,
∴OD∥AC,
∵DE⊥AC,
∴OD⊥DE,
∴DE为⊙O的切线;
(2)解:∵AB为直径,
∴∠AFB=90°,
∵∠EGF=∠AGF,
∴Rt△GEF∽△Rt△GAE,
∴![]() ,即
,即![]()
整理得GF2+3GF﹣4=0,解得GF=1或GF=﹣4(舍去),
在Rt△AEG中,sin∠EAG![]()
∴∠EAG=30°,
即∠EAF的度数为30°.


科目:初中数学 来源: 题型:
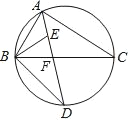
【题目】如图,∠BAC的平分线交AABC的外接圆于点D,交BC于点F,∠ABC的平分线交AD于点E.
(1)求证:DE=DB.
(2)若∠BAC=90°,BD=4,求△ABC外接圆的半径;
(3)若BD=6,DF=4,求AD的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 这五个数中,任取一个数作为
这五个数中,任取一个数作为![]() 的值,恰好使得关于
的值,恰好使得关于![]() 的一元二次方程
的一元二次方程![]() 有两个不相等的实数根,且使两个根都在
有两个不相等的实数根,且使两个根都在![]() 和
和![]() 之间(包括
之间(包括![]() 和
和![]() ),则取到满足条件的
),则取到满足条件的![]() 值的概率为________.
值的概率为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
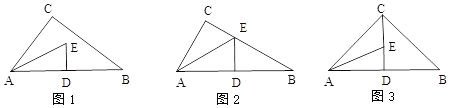
【题目】如图1,△ABC是直角三角形,∠C=90°,∠CAB的角平分线AE与 AB的垂直平分线DE相交于点E.
(1)如图2,若点E正好落在边BC上.
①求∠B的度数
②证明:BC=3DE
(2)如图3,若点E满足C、E、D共线.
求证:AD+DE=BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(﹣4,![]() ),B(﹣1,m)是一次函数y=kx+b与反比例函数y=
),B(﹣1,m)是一次函数y=kx+b与反比例函数y=![]() 图象的两个交点,AC⊥x轴于点C,BD⊥y轴于点D.
图象的两个交点,AC⊥x轴于点C,BD⊥y轴于点D.
(1)求m的值及一次函数解析式;
(2)P是线段AB上的一点,连接PC、PD,若△PCA和△PDB面积相等,求点P坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是菱形ABCD的对角线的交点,E、F分别是OA、OC的中点,下列结论:①四边形BFDE是菱形;②S四边形ABCD=EF×BD;③∠ADE=∠EDO;④△DEF是轴对称图形.其中正确的结论有( )
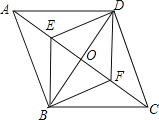
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两同学的家与学校的距离均为3200米.甲同学先步行200米,然后乘公交车去学校,乙同学骑自行车去学校.已知甲步行速度是乙骑自行车速度的![]() ,公交车的速度是乙骑自行车速度的3倍.甲、乙两同学同时从家出发去学校,结果甲同学比乙同学早到8分钟.
,公交车的速度是乙骑自行车速度的3倍.甲、乙两同学同时从家出发去学校,结果甲同学比乙同学早到8分钟.
(1)求乙骑自行车的速度;
(2)当甲到达学校时,乙同学离学校还有多远?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com