
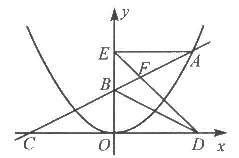
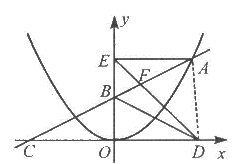
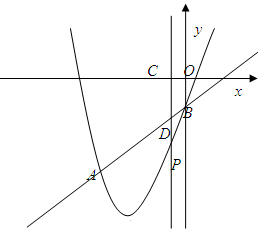
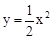 上的一个动点,且点A在第一象限内.AE⊥y轴于点E,点B坐标为(O,2),直线AB交
上的一个动点,且点A在第一象限内.AE⊥y轴于点E,点B坐标为(O,2),直线AB交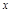 轴于点C,点D与点C关于y轴对称,直线DE与AB相交于点F,连结BD.设线段AE的长为m,△BED的面积为S.
轴于点C,点D与点C关于y轴对称,直线DE与AB相交于点F,连结BD.设线段AE的长为m,△BED的面积为S.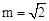 时,求S的值.
时,求S的值.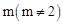 的函数解析式.
的函数解析式.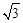 时,求
时,求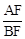 的值;
的值;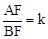 ,猜想k与m的数量关系并证明.
,猜想k与m的数量关系并证明.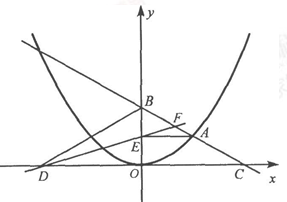
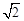 ;(2)
;(2)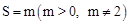 ;(3)①
;(3)① ;②
;②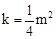 ,证明见解析.
,证明见解析.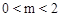 和
和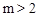 两种情况讨论.
两种情况讨论.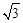 求出
求出 现,得到点A 的坐标,应用待定系数法,设
现,得到点A 的坐标,应用待定系数法,设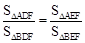
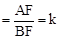 得到
得到 ,从而
,从而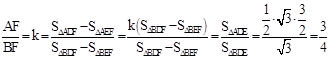 .
.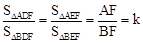 得到
得到 ,从而得到
,从而得到 ,因此
,因此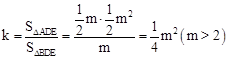 .
.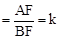 得到
得到 ,从而
,从而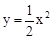 上的一个动点,AE⊥y轴于点E,且
上的一个动点,AE⊥y轴于点E,且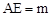 ,
, . ∴当
. ∴当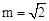 时,点A的坐标为
时,点A的坐标为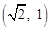 .
.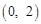 ,∴BE=OE=1.
,∴BE=OE=1.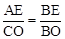 ,即
,即 ,解得
,解得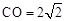 .
.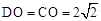 .
. .
.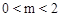 时,如图,
时,如图,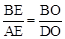 .∴
.∴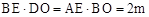
 .
.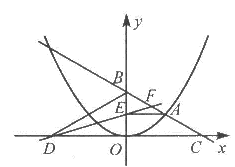
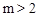 时,如图,同①可得
时,如图,同①可得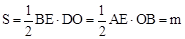
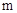 的函数解析式
的函数解析式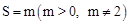 .
.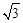 ,∴
,∴ .∴点A 的坐标为
.∴点A 的坐标为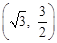 .
.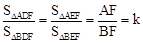 ,∴
,∴ .
.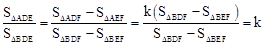 .
. .
.
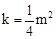 ,证明如下:
,证明如下: ,∴
,∴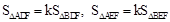 .
.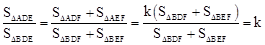 .
. ,∴
,∴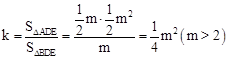 .
.


 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源:不详 题型:解答题
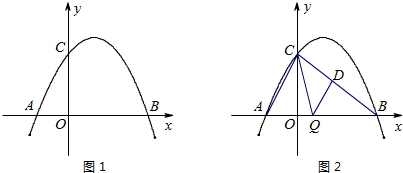
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
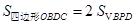 ;
;
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
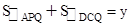 ,写出y与t之间的函数解析式,并探究P点运动到第几秒到第几秒之间时,y取得最小值.
,写出y与t之间的函数解析式,并探究P点运动到第几秒到第几秒之间时,y取得最小值.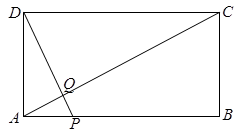
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 ;④3≤n≤4中,正确的是( )。
;④3≤n≤4中,正确的是( )。
| A.①② | B.③④ | C.①④ | D.①③ |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 的图象如图所示,其对称轴为直线x=-1,与x轴的一个交点为(1,0),与y轴的交点在(0,2)与(0,3)之间(不包含端点),则下列结论正确的是( )
的图象如图所示,其对称轴为直线x=-1,与x轴的一个交点为(1,0),与y轴的交点在(0,2)与(0,3)之间(不包含端点),则下列结论正确的是( )
A. | B. | C. | D. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com