
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:
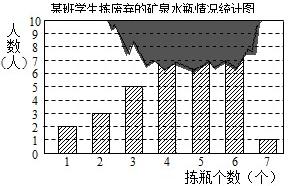 4、如图为某班35名学生在某次社会实践活动中拣废弃的矿泉水瓶情况条形统计图,图中上面部分数据破损导致数据不完全.已知此次活动中学生拣到矿泉水瓶个数中位数是5个,则根据统计图,下列选项中的( )数值无法确定.
4、如图为某班35名学生在某次社会实践活动中拣废弃的矿泉水瓶情况条形统计图,图中上面部分数据破损导致数据不完全.已知此次活动中学生拣到矿泉水瓶个数中位数是5个,则根据统计图,下列选项中的( )数值无法确定.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com