
【题目】如图,已知A(3,1),B(-2,3),线段AB与y轴相交于点C.

(1)求△AOB的面积;
(2)求点C的坐标;
(3)请直接写出直线AB与x轴的交点坐标.
【答案】(1)S△AOB=![]() ;(2)C(0,
;(2)C(0,![]() );(3)直线AB与x轴交点为(
);(3)直线AB与x轴交点为(![]() ,0);
,0);
【解析】
(1)过A作AE⊥x轴于E,过B作BF⊥x轴于F,S△AOB=S梯形AEFB-S△AOE-S△FOB=![]() -
-![]() -
-![]() =
=![]() ;
;
(2)S△AOB=S△AOC+S△COB,则有![]() =
=![]() OB×3+
OB×3+![]() ,即可求OC;
,即可求OC;
(3)设直线AB的解析式y=kx+b,将A(3,1),B(-2,3)代入,即可得y=-![]() x+
x+![]() ;
;
解:(1)过A作AE⊥x轴于E,过B作BF⊥x轴于F,
,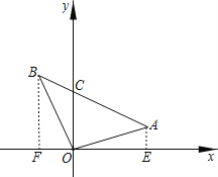
∵A(3,1),B(-2,3),
∴AE=1,BF=OE=3,FO=2,
∴EF=5,
∴S△AOB=S梯形AEFB-S△AOE-S△FOB=![]() -
-![]() -
-![]() =
=![]() ;
;
(2)∵S△AOB=S△AOC+S△COB,
∴![]() =
=![]() OB×3+
OB×3+![]() ,
,
∴OC=![]() ,
,
∴C(0,![]() );
);
(3)设直线AB的解析式y=kx+b,
将A(3,1),B(-2,3)代入,
∴![]() ,
,
∴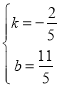 ,
,
∴y=-![]() x+
x+![]() ,
,
∴直线AB与x轴交点为(![]() ,0);
,0);


科目:初中数学 来源: 题型:
【题目】如图,甲、乙两图是分别由五个棱长为“1”的立方块组成的两个几何体,它们的三视图中完全一致的是
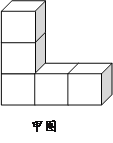
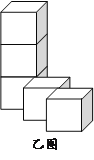
A. 三视图都一致 B. 主视图 C. 俯视图 D. 左视图
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家电销售商城电冰箱的销售价为每台2100元,空调的销售价为每台1750元,每台电冰箱的进价比每台空调的进价多400元,商城用80000元购进电冰箱的数量与用64000元购进空调的数量相等.
求每台电冰箱与空调的进价分别是多少?
(2)现在商城准备一次购进这两种家电共100台,设购进电冰箱x台,这100台家电的销售总利润为y元,要求购进空调数量不超过电冰箱数量的2倍,总利润不低于13000元,请分析合理的方案共有多少种?并确定获利最大的方案以及最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线 ![]() :y=2x+1与直线
:y=2x+1与直线 ![]() :y=mx+4相交于点P(1,b)
:y=mx+4相交于点P(1,b)
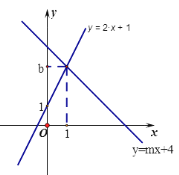
(1)求b,m的值
(2)垂直于x轴的直线 x=a与直线 ![]() ,
,![]() 分别相交于C,D,若线段CD长为2,求a的值
分别相交于C,D,若线段CD长为2,求a的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AM∥CN,点B为平面内一点,AB⊥BC于B.

(1)如图1,直接写出∠A和∠C之间的数量关系___;
(2)如图2,过点B作BD⊥AM于点D,求证:∠ABD=∠C;
(3)如图3,在(2)问的条件下,点E. F在DM上,连接BE、BF、CF,BF平分∠DBC,BE平分∠ABD,若∠FCB+∠NCF=180°,∠BFC=3∠DBE,求∠EBC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,过点
中,过点![]() 的直线交
的直线交![]() 轴正半轴于点
轴正半轴于点![]() ,将直线
,将直线![]() 绕着点
绕着点![]() 顺时针旋转
顺时针旋转![]() 后,分别与
后,分别与![]() 轴
轴![]() 轴交于点
轴交于点![]() 、
、![]() .
.
(1)若![]() ,求直线
,求直线![]() 的函数关系式;
的函数关系式;
(2)连接![]() ,若
,若![]() 的面积是5,求点
的面积是5,求点![]() 的运动路径长.
的运动路径长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017江苏省宿迁市,第25题,10分)如图,在平面直角坐标系xOy中,抛物线![]() 交x轴于A,B两点(点A在点B的左侧),将该抛物线位于x轴上方曲线记作M,将该抛物线位于x轴下方部分沿x轴翻折,翻折后所得曲线记作N,曲线N交y轴于点C,连接AC、BC.
交x轴于A,B两点(点A在点B的左侧),将该抛物线位于x轴上方曲线记作M,将该抛物线位于x轴下方部分沿x轴翻折,翻折后所得曲线记作N,曲线N交y轴于点C,连接AC、BC.
(1)求曲线N所在抛物线相应的函数表达式;
(2)求△ABC外接圆的半径;
(3)点P为曲线M或曲线N上的一动点,点Q为x轴上的一个动点,若以点B,C,P,Q为顶点的四边形是平行四边形,求点Q的坐标.
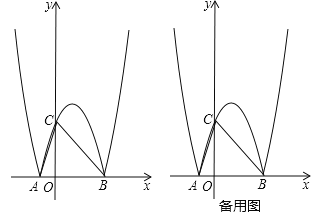
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点O是平行四边形ABCD的对称中心,AD>AB,E、F分别是AB边上的点,且EF=![]() AB;G、H分别是BC边上的点,且GH=
AB;G、H分别是BC边上的点,且GH=![]() BC;若S1,S2分别表示EOF和GOH的面积,则S1,S2之间的等量关系是______________
BC;若S1,S2分别表示EOF和GOH的面积,则S1,S2之间的等量关系是______________
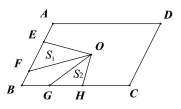
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在Rt△ABC中,∠ACB=90°,AC=4,BC=2,D是AC边上的一个动点,将△ABD沿BD所在直线折叠,使点A落在点P处.
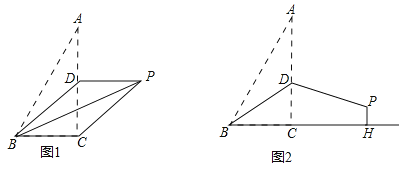
(1)如图1,若点D是AC中点,连接PC.
①写出BP,BD的长;
②求证:四边形BCPD是平行四边形.
(2)如图2,若BD=AD,过点P作PH⊥BC交BC的延长线于点H,求PH的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com