
【题目】如图,四边形ABCD中,AD∥BC,BA⊥AD,BC=DC,BE⊥CD于点E. 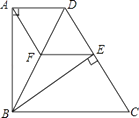
(1)求证:△ABD≌△EBD;
(2)过点E作EF∥DA,交BD于点F,连接AF.求证:四边形AFED是菱形.
【答案】
(1)证明:如图,

∵AD∥BC,
∴∠1=∠DBC.
∵BC=DC,
∴∠2=∠DBC.
∴∠1=∠2.
∵BA⊥AD,BE⊥CD
∴∠BAD=∠BED=90°,
在△ABD和△EBD中  ,
,
∴△ABD≌△EBD(AAS)
(2)证明:由(1)得,AD=ED,∠1=∠2.
∵EF∥DA,
∴∠1=∠3.
∴∠2=∠3.
∴EF=ED.
∴EF=AD.
∴四边形AFED是平行四边形.
又∵AD=ED,
∴四边形AFED是菱形.
【解析】(1)首先证明∠1=∠2.再由BA⊥AD,BE⊥CD可得∠BAD=∠BED=90°,然后再加上公共边BD=BD可得△ABD≌△EBD;(2)首先证明四边形AFED是平行四边形,再有AD=ED,可得四边形AFED是菱形.
【考点精析】根据题目的已知条件,利用菱形的判定方法的相关知识可以得到问题的答案,需要掌握任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形.


科目:初中数学 来源: 题型:
【题目】美丽的惠东是广东省的海洋大县,海域面积约3200平方公里,这个数据用科学记数法表示为( )平方公里.
A. 3.2×102B. 32×102C. 3.2×103D. 0.32×103
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B为定点,定直线l∥AB,P是l上一动点,点M,N分别为PA,PB的中点,对下列各值: ①线段MN的长;②△PAB的周长;③△PMN的面积;④直线MN,AB之间的距离;⑤∠APB的大小.
其中会随点P的移动而变化的是( )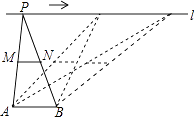
A.②③
B.②⑤
C.①③④
D.④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
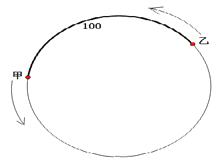
【题目】已知甲沿周长为300米的环形跑道上按逆时针方向跑步,速度为![]() 米/秒,与此同时在甲后面100米的乙也沿该环形跑道按逆时针方向跑步,速度为3米/秒.设运动时间为
米/秒,与此同时在甲后面100米的乙也沿该环形跑道按逆时针方向跑步,速度为3米/秒.设运动时间为![]() 秒.
秒.
(1)若![]() =5,求甲、乙两人第1次相遇的时间;
=5,求甲、乙两人第1次相遇的时间;
(2)当![]() 时,甲、乙两人第1次相遇.
时,甲、乙两人第1次相遇.
①求![]() 的值;
的值;
②若![]() 时,甲、乙两人第1次相遇前,当两人相距120米时,求
时,甲、乙两人第1次相遇前,当两人相距120米时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,边AB的长为3,点E,F分别在AD,BC上,连接BE,DF,EF,BD.若四边形BFDE是菱形,且OE=AE,则边BC的长为( ) 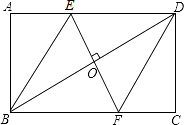
A.2 ![]()
B.3 ![]()
C.![]()
![]()
D.6 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连结AC交EF于G,下列结论:①BE=DF;②∠AEF=15°;③AC垂直平分EF;④BE+DF=EF;⑤△CEF为等腰直角三角形,其中正确的有(填序号). 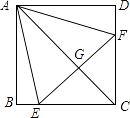
查看答案和解析>>
科目:初中数学 来源: 题型:
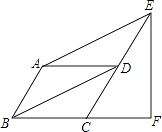
【题目】如图,平行四边形ABCD中,∠ABC=60°,点E,F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,CF= ![]() .
. 
(1)求证:四边形ABDE是平行四边形;
(2)求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两个商场以同样的价格出售同样的商品,并且又各自推出不同的优惠措施,甲商场的优惠措施是:累计购买100元商品后,再买的商品按原价的90%收费;乙商场则是:累计购买50元商品后,再买商品按原价的95%收费,顾客选择哪个商店购物获得更多的优惠?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com