【题目】某公园划船项目收费标准如下：某班18名同学一起去该公园划船，若每人划船的时间均为1小时，则租船的总费用最低为_____元．
船型 | 两人船（限乘两 人） | 四人船（限乘四 人） | 六人船（限乘六 人） | 八人船（限乘八 人） |
每船租金（元/小时） | 50 | 80 | 100 | 120 |
科目：初中数学 来源： 题型：
【题目】下列调查中，适合采用全面调查（普查）方式的是（ ）
A.对汀江流域水质情况的调查B.对端午节期间市场上粽子质量情况的调查
C.对某班
名同学身高情况的调查D.对某类烟花爆竹燃放安全情况的调查
查看答案和解析>>
科目：初中数学 来源： 题型：
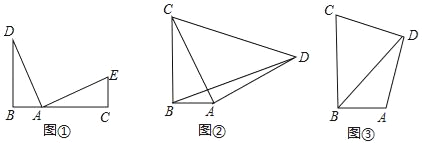
【题目】（1）观察猜想
如图①点B、A、C在同一条直线上，DB⊥BC，EC⊥BC且∠DAE=90°，AD=AE，则BC、BD、CE之间的数量关系为；
（2）问题解决
如图②，在Rt△ABC中，∠ABC=90°，CB=4，AB=2，以AC为直角边向外作等腰Rt△DAC，连结BD，求BD的长；
（3）拓展延伸
如图③，在四边形ABCD中，∠ABC=∠ADC=90°，CB=4，AB=2，DC=DA，请直接写出BD的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，二次函数y＝ax2+4x+c的图象与x轴交于A、B两点，与y轴交于点C，其中A（﹣1，0），C（0，5）
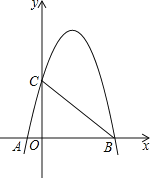
（1）求二次函数的解析式，并求出当x＝1时的函数值．
（2）连接BC，AC，得到△ABC，现将抛物线图象只向下平移m个单位，使得顶点落在△ABC内部（不包括边界），请写出m的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AB是⊙O的直径，BC交⊙O于点D，E是
的中点，连接AE交BC于点F，∠ACB=2∠EAB．
（1）求证：AC是⊙O的切线；
（2）若cosC=
，AC=6，求BF的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AB=AC，∠ABC=70°，以B为圆心，任意长为半径画弧交AB，BC于点E，F，再分别以点E，F为圆心、以大于
EF长为半径画弧，两弧交于点P，作射线BP交AC于点D，则∠BDC为（ ）度．
A. 65 B. 75 C. 80 D. 85
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读材料，解答问题：
观察下列方程：①
；②
；③
；…；
（1）按此规律写出关于x的第4个方程为 ，第n个方程为 ；
（2）直接写出第n个方程的解，并检验此解是否正确．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】对于反比例函数y=
（k≠0），下列所给的四个结论中，正确的是（ ）
A. 若点（3，6）在其图象上，则（﹣3，6）也在其图象上
B. 当k＞0时，y随x的增大而减小
C. 过图象上任一点P作x轴、y轴的线，垂足分别A、B，则矩形OAPB的面积为k
D. 反比例函数的图象关于直线y=﹣x成轴对称
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
