
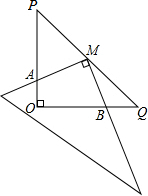
 如图,在Rt△POQ中,OP=OQ=4,M是PQ的中点,把一三角尺的直角顶点放在M处,以M为旋转中心,旋转三角尺、三角尺的两直角边与与△POQ的两直角边分别交于点A、B.
如图,在Rt△POQ中,OP=OQ=4,M是PQ的中点,把一三角尺的直角顶点放在M处,以M为旋转中心,旋转三角尺、三角尺的两直角边与与△POQ的两直角边分别交于点A、B.分析 (1)过点M作ME⊥OP于点E,作MF⊥OQ于点F,可得四边形OEBF是矩形,根据三角形的中位线定理可得ME=MF,再根据同角的余角相等可得∠AME=∠BMF,再利用“角边角”证明△AME和△BMF全等,根据全等三角形对应边相等即可证明;
(2)连接OM,证明△AMO≌△BMQ,得到OA=QB,所以OP=OQ=OB+BQ=OB+OA.
(3)根据全等三角形对应边相等可得AE=BF,设OA=x,表示出AE为2-x,即BF的长度,然后表示出OB=2+(2-x),再利用勾股定理列式求出AM,然后根据等腰直角三角形的斜边等于直角边的$\sqrt{2}$倍表示出AB的长度,然后根据三角形的周长公式列式判断出△AOB的周长随AB的变化而变化,再根据二次函数的最值问题求出周长最小时的x的值,然后解答即可.
解答 解:(1)如图1,过点M作ME⊥OP于点E,作MF⊥OQ于点F,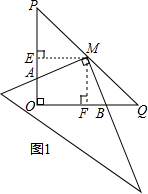
∵∠O=90°,
∴四边形OEMF是矩形,
∵M是PQ的中点,OP=OQ=4,∠O=90°,
∴ME=$\frac{1}{2}$OQ=2,MF=$\frac{1}{2}$OP=2,
∴ME=MF,
∴四边形OEMF是正方形,
∵∠AME+∠AMF=90°,∠BMF+∠AMF=90°,
∴∠AME=∠BMF,
在△AME和△BMF中,
$\left\{\begin{array}{l}{∠AME=∠BMF}\\{ME=MF}\\{∠AEM=∠BFM}\end{array}\right.$,
∴△AME≌△BMF(ASA),
∴MA=MB
(2)OA+OB=OP
如图2,连接MO,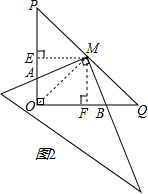
在Rt△POQ中,
∵OP=OQ,M是PQ中点,
∴OM⊥PQ,
∴∠OMP=90°
即∠OMA+AMP=90°,
∵∠AMB=90°,
∴∠BMQ+∠AMP=90°,
∴∠OMA=∠BMQ
在Rt△POQ中,由勾股定理得PQ=4$\sqrt{2}$,PM=QP=$\frac{1}{2}$PQ=$\sqrt{2}$,
在△POM中,∵∠OMP=90°,∠P=45°,
∴∠POM=45°,
∴OM=PM=QM=2$\sqrt{2}$,
在△AMO与△BMQ中,
$\left\{\begin{array}{l}{AM=BM}\\{∠OMA=∠BMQ}\\{OM=QM}\end{array}\right.$,
∴△AMO≌△BMQ(SAS),
∴OA=QB,
∴OP=OQ=OB+BQ=OB+OA.
(3)根据(1)中的△AME≌△BMF得到:AE=BF,
设OA=x,则AE=2-x,
∴OB=OF+BF=2+(2-x)=4-x,
在Rt△AME中,AM=$\sqrt{A{E}^{2}+M{E}^{2}}$=$\sqrt{(2-x)^{2}+{2}^{2}}$,
∵∠AMB=90°,MA=MB,
∴AB=$\sqrt{2}$AM=$\sqrt{2}$•$\sqrt{(2-x)^{2}+{2}^{2}}$=$\sqrt{2(2-x)^{2}+8}$,
∴△AOB的面积=$\frac{1}{2}$OA•OB=$\frac{1}{2}$x•(4-x)=-$\frac{1}{2}$(x-2)2+4,
∴当x=2时,即点A为OP的中点时,△AOB的面积有最大值,最大值为4.
△AOB的周长=OA+OB+AB=x+(4-x)+$\sqrt{2(2-x)^{2}+8}$=4+$\sqrt{2(2-x)^{2}+8}$,
所以,当x=2,即点A为OP的中点时,△AOB的周长有最小值,最小值为4+$\sqrt{8}$,即4+2$\sqrt{2}$.
点评 本题考查了全等三角形的判定与性质,等腰直角三角的性质,三角形的中位线定理,勾股定理的应用,以及二次函数的最值问题,作出辅助线,把动点问题转化为固定的三角形,构造出全等三角形是解题的关键,也是本题的难点.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com