
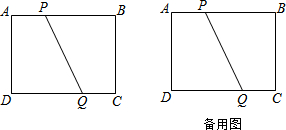
分析 (1)根据已知条件,证明四边形APQD是矩形,再根据矩形的性质和AP=CQ求x即可;
(2)连接EP、EQ,则EP=EQ,设BE=y,列出等式(8-x)2+y2=(6-y)2+x2然后根据函数的性质来求x的取值范围;
(3)由图形的等量关系列出方程,再根据函数的性质来求最值.
解答 解:(1)当PQ∥AD时,则
∠A=∠APQ=90°,∠D=∠DQP=90°,
又∵AB∥CD,
∴四边形APQD是矩形,
∴AP=QD,
∵AP=CQ,
AP=$\frac{1}{2}$CD=$\frac{1}{2}$×8=4,
∴x=4.
故答案为:4.
(2)如图,连接EP、EQ,则EP=EQ,设BE=y.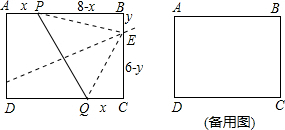
∴(8-x)2+y2=(6-y)2+x2,
∴y=$\frac{4x-7}{3}$.
∵0≤y≤6,
∴0≤$\frac{4x-7}{3}$≤6,
$\frac{7}{4}$≤x≤$\frac{25}{4}$.
(3)S△BPE=$\frac{1}{2}$•BE•BP=$\frac{1}{2}$•(8-x)•$\frac{4x-7}{3}$=$\frac{-4{x}^{2}+39x-56}{6}$,
S△ECQ=$\frac{1}{2}$•CE•CQ=$\frac{1}{2}$•(6-$\frac{4x-7}{3}$)•x=$\frac{-4{x}^{2}+25x}{6}$,
∵AP=CQ,
∴SBPQC=$\frac{1}{2}$S矩形ABCD=24,
∴S=SBPQC-S△BPE-S△ECQ=24-$\frac{-4{x}^{2}+39x-56}{6}$-$\frac{-4{x}^{2}+25x}{6}$,
整理得:S=$\frac{4{x}^{2}-32x+100}{3}$=$\frac{4}{3}$(x-4)2+12($\frac{7}{4}≤x≤\frac{25}{4}$),
∴当x=4时,S有最小值12,
当x=$\frac{7}{4}$或x=$\frac{25}{4}$时,S有最大值$\frac{75}{4}$.
∴12≤S≤$\frac{75}{4}$.
故答案为:S=$\frac{4}{3}$(x-4)2+12($\frac{7}{4}≤x≤\frac{25}{4}$).
点评 考查了四边形综合题,解答本题时,涉及到了矩形的判定、矩形的性质、勾股定理以及二次函数的最值等知识点,这是一道综合性比较强的题目,所以在解答题目时,一定要把各个知识点融会贯通,这样解题时才会少走弯路.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
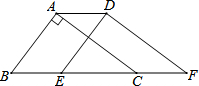 如图,在△ABC中,∠BAC=90°,AB=3,AC=4,BC=5,将△ABC沿直线BC向右平移2个单位得到△DEF,连接AD,则下列结论:
如图,在△ABC中,∠BAC=90°,AB=3,AC=4,BC=5,将△ABC沿直线BC向右平移2个单位得到△DEF,连接AD,则下列结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,AB=AC,AD⊥BC于D点,点E、F是线段AD上的三等分点,连接BE、CE、BF、CF,若$\frac{BC}{AD}=\frac{2}{3}$,且BC=4a.
如图,在△ABC中,AB=AC,AD⊥BC于D点,点E、F是线段AD上的三等分点,连接BE、CE、BF、CF,若$\frac{BC}{AD}=\frac{2}{3}$,且BC=4a.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
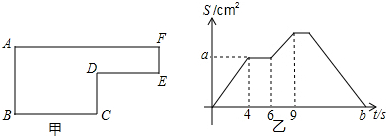
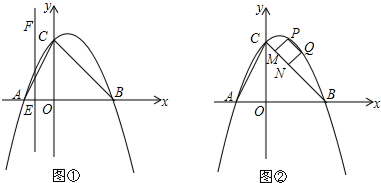
| A. | 图1中BC的长是4厘米 | B. | 图2中的a是12 | ||
| C. | 图1中的图形面积是60平方厘米 | D. | 图2中的b是19 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com