

分析 (1)作出辅助线,先判断出△DGE≌△DOC,得出EG=OC,再判断出EG=AE即可;
(2)根据S△DCO=S△ADE可知S△DCO+S四边形DOBE=S△ADE+S四边形DOBE,从而得到S△BCE=S△AOB,
根据△AOB为正三角形求出三角形的高,从而求出A点坐标,根据待定系数法求出AB的解析式,根据S△BCE=S△AOB,求出A点纵坐标,代入直线AB,可得E点横坐标,再利用待定系数法求出CD的解析式;
(3)作出辅助线先判断出△FDO≌△FDN,进而判断出FO=FB,再求出∠OFB=30°,用等腰三角形的旋转求出点F的坐标.
解答 解:(1)如图(1),
过点E作EG∥OB,
∴∠AGE=∠AOB,
∴∠DGE=∠DOC,
在△DGE和△DOC中,$\left\{\begin{array}{l}{∠DGE=∠DOC}\\{∠GDE=∠ODC}\\{DE=CD}\end{array}\right.$,
∴△DGE≌△DOC,
∴EG=OC,
∵△AOB是等边三角形,EG∥OB,
∴△AEG是等边三角形,
∴AE=EG=OC,
(2)∵m=-2,
∴C(-2,0)
∵S△DCO=S△ADE,
∴S△DCO+S四边形DOBE=S△ADE+S四边形DOBE,
∴S△BCE=S△AOB,
∵△AOB为正三角形,B坐标为(2,0)知其边长为2,高为$\sqrt{3}$,
∴点A(1,$\sqrt{3}$).
∴S△AOB=$\frac{1}{2}$×2×$\sqrt{3}$=$\sqrt{3}$.
设E(x0,y0),则S△CBE=$\frac{1}{2}$×4×y0=2y0,
∵2y0=$\sqrt{3}$,
∴y0=$\frac{\sqrt{3}}{2}$,
由点A(1,$\sqrt{3}$),B(2,0)得直线AB解析式为y=-$\sqrt{3}$(x-2),
而E在直线AB上,则y0=-$\sqrt{3}$(x0-2),
可得,x0=$\frac{3}{2}$,
∴点E($\frac{3}{2}$,$\frac{\sqrt{3}}{2}$),
又∵点C(-2,0),
∴$\left\{\begin{array}{l}{\frac{3}{2}k+b=\frac{\sqrt{3}}{2}}\\{-2k+b=0}\end{array}\right.$,
∴$\left\{\begin{array}{l}{k=\frac{\sqrt{3}}{7}}\\{b=\frac{2\sqrt{3}}{7}}\end{array}\right.$,
∴直线l的解析式为:y=$\frac{\sqrt{3}}{7}$x+$\frac{2\sqrt{3}}{7}$.
(3)如图(2),
连接FB,FO,在DE上截取DN=DO,
∵OD+BE=DE,DE=DN+EN,
∴EN=EB,
∵∠ODE与∠BED的平分线交于点F,
∴∠ODF=∠NDF
在△FDO和△FDN中$\left\{\begin{array}{l}{DO=DN}\\{∠ODF=∠NDF}\\{DF=DF}\end{array}\right.$,
∴△FDO≌△FDN,
∴∠DFO=∠DFN,FO=FN,
同理:∠NFE=∠BFE,FN=FB,
∴FO=FB,
∵∠DFE=90°-$\frac{1}{2}$∠A=60°,
∴∠OFB=2∠DFE=120°,
∴∠BOF=30°,
过点F作FM⊥OB,
∴OM=$\frac{1}{2}$OB=1,
在Rt△OMF中,tan30°=$\frac{FM}{OM}$=$\frac{FM}{1}$=$\frac{\sqrt{3}}{3}$,
∴FM=$\frac{\sqrt{3}}{3}$,
∴F(1,-$\frac{\sqrt{3}}{3}$).
点评 此题是一次函数综合题,主要考查了全等三角形的判定和性质,等边三角形,等腰三角形的判定和性质,角平分线的应用,解本题的关键是S△BCE=S△AOB,和判断出FO=FB.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{a+3}{2}$ | B. | $\frac{a-3}{2}$ | C. | -$\frac{a+3}{2}$ | D. | $\frac{3-a}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 没有θ的值可适合 | B. | 仅当θ=45° | ||
| C. | 仅当0°<θ≤45° | D. | 仅当45°≤θ<60° | ||
| E. | 对于所有满足0°<θ<60°的θ都适合 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,分别以五边形ABCDE的顶点为圆心,以1为半径作五个圆,则图中阴影部分的面积之和为( )
如图,分别以五边形ABCDE的顶点为圆心,以1为半径作五个圆,则图中阴影部分的面积之和为( )| A. | $\frac{3}{2}π$ | B. | 3π | C. | $\frac{7}{2}π$ | D. | 2π |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 200元,150元 | B. | 210元,280元 | C. | 280元,210元 | D. | 150元,200元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,∠ACB=90°,∠A=30°,AB的垂直平分线分别交AB和AC于点D,E.
如图,在△ABC中,∠ACB=90°,∠A=30°,AB的垂直平分线分别交AB和AC于点D,E.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
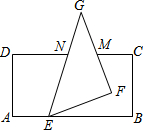 如图,将一张长方形纸片与一张直角三角形纸片(∠EFG=90°)按如图所示的位置摆放,使直角三角形纸片的一个顶点E恰好落在长方形纸片的一边AB上,已知∠BEF=21°,则∠CMF=69°.
如图,将一张长方形纸片与一张直角三角形纸片(∠EFG=90°)按如图所示的位置摆放,使直角三角形纸片的一个顶点E恰好落在长方形纸片的一边AB上,已知∠BEF=21°,则∠CMF=69°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com