
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{60}{x}$=$\frac{50}{x-5}$ | B. | $\frac{50}{x}$=$\frac{60}{x-5}$ | C. | $\frac{60}{x}$=$\frac{50}{x+5}$ | D. | $\frac{50}{x}$=$\frac{60}{x+5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
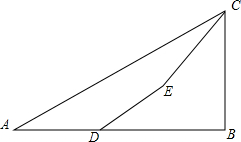 如图,为了测量某建筑物BC的高度,小明先在地面上用测角仪自A处测得建筑物顶部的仰角是30°,然后在水平地而上向建筑物前进了50m到达D处,此时遇到一斜坡,坡度i=1:$\sqrt{3}$,沿着斜坡前进20米到达E处测得建筑物顶部的仰角是45°,(坡度i=1:$\sqrt{3}$是指坡面的铅直高度FE与水平宽度DE的比).请你计算出该建筑物BC的高度.(取$\sqrt{3}$=1.732,结果精确到0.1m).
如图,为了测量某建筑物BC的高度,小明先在地面上用测角仪自A处测得建筑物顶部的仰角是30°,然后在水平地而上向建筑物前进了50m到达D处,此时遇到一斜坡,坡度i=1:$\sqrt{3}$,沿着斜坡前进20米到达E处测得建筑物顶部的仰角是45°,(坡度i=1:$\sqrt{3}$是指坡面的铅直高度FE与水平宽度DE的比).请你计算出该建筑物BC的高度.(取$\sqrt{3}$=1.732,结果精确到0.1m).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
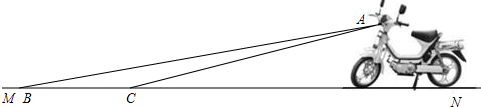
 如图,在一条笔直的东西向海岸线l上有一长为1.5km的码头MN和灯塔C,灯塔C距码头的东端N有20km.一轮船以36km/h的速度航行,上午10:00在A处测得灯塔C位于轮船的北偏西30°方向,上午10:40在B处测得灯塔C位于轮船的北偏东60°方向,且与灯塔C相距12km.
如图,在一条笔直的东西向海岸线l上有一长为1.5km的码头MN和灯塔C,灯塔C距码头的东端N有20km.一轮船以36km/h的速度航行,上午10:00在A处测得灯塔C位于轮船的北偏西30°方向,上午10:40在B处测得灯塔C位于轮船的北偏东60°方向,且与灯塔C相距12km.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com