
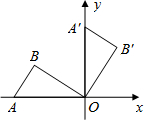
 如图,将放置于平面直角坐标系中的三角板AOB绕O点顺时针旋转90°得△A′OB′.已知∠AOB=30°,∠B=90°,AB=1.
如图,将放置于平面直角坐标系中的三角板AOB绕O点顺时针旋转90°得△A′OB′.已知∠AOB=30°,∠B=90°,AB=1.分析 (1)根据直角三角形30°角所对的直角边等于斜边的一半可得OA=2AB,再求出OB,根据旋转的性质可得OB′=OB,过点B′作B′C⊥x轴于C,求出∠COB′=60°,然后求出OC、B′C,再根据点的坐标的定义求解即可;
(2)根据旋转的性质可得OA′=OA,然后写出点A′的坐标,再根据关于原点对称的点的横坐标与纵坐标都互为相反数求解.
解答 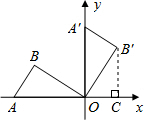 解:(1)∵∠AOB=30°,∠B=90°,
解:(1)∵∠AOB=30°,∠B=90°,
∴OA=2AB=2×1=2,
OB=$\sqrt{3}$AB=$\sqrt{3}$,
∵△AOB绕O点顺时针旋转90°得△A′OB′,
∴OB′=OB=$\sqrt{3}$,
过点B′作B′C⊥x轴于C,
则∠COB′=180°-30°-90°=60°,
∴OC=$\frac{1}{2}$OB′=$\frac{\sqrt{3}}{2}$,
B′C=$\frac{\sqrt{3}}{2}$OB′=$\frac{\sqrt{3}}{2}$×$\sqrt{3}$=$\frac{3}{2}$,
所以,点B′的坐标为($\frac{\sqrt{3}}{2}$,$\frac{3}{2}$);
(2)∵△AOB绕O点顺时针旋转90°得△A′OB′,
∴OA′=OA=2,
∴点A′的坐标为(0,2),
∴△A′OB′关于原点成中心对称的三角形的顶点坐标分别为(0,-2),(0,0),(-$\frac{\sqrt{3}}{2}$,-$\frac{3}{2}$).
点评 本题考查了坐标与图形的变化-旋转,直角三角形30°角所对的直角边等于斜边的一半的性质,关于原点对称的点的坐标特征,解题的关键在于作出以点B′为顶点的直角三角形.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 试验次数 | 20 | 80 | 100 | 160 | 200 | 240 | 300 | 360 | 400 |
| “车”字朝上的频数 | 14 | 48 | 50 | 84 | 112 | 144 | 172 | 204 | 228 |
| 相应的频率 | 0.70 | 0.60 | 0.50 | 0.53 | 0.56 | 0.60 | 0.57 | 0.57 | 0.57 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com