
【题目】如图,反比例函数y=![]() (x>0)过点A(3,4),直线AC与x轴交于点C(6,0),过点C作x轴的垂线BC交反比例函数图象于点B.
(x>0)过点A(3,4),直线AC与x轴交于点C(6,0),过点C作x轴的垂线BC交反比例函数图象于点B.
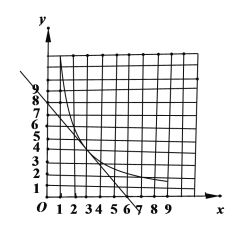
(1)填空:反比例函数的解析式为____________________,直线AC的解析式为____________________,B点的坐标是________.
(2)在平面内有点D,使得以A,B,C,D四点为项点的边形为平行四边形.
①在图中用直尺和2B铅笔画出所有符合条件的平行四边形;
②根据所画形,请直接写出符合条件的所有点D的坐标.
【答案】(1)![]() ,
,![]() ,(6,2);(2)①见解析,② (3,6)、(3,2)、(9,-2)
,(6,2);(2)①见解析,② (3,6)、(3,2)、(9,-2)
【解析】
(1)由待定系数法求解析式,将x=6代入反比例函数解析式可求点B坐标;
(2)①如图,分别以AB,BC和AC为对角线画出平行四边形;
②由图形可求解.
解:(1)∵反比例函数![]() 过点A(3,4),
过点A(3,4),
∴k=3×4=12
故反比例函数的解析式为:![]() .
.
设直线AC的解析式为:y=ax+b
由题意得:![]() ,解之得
,解之得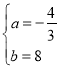
∴一次函数的解析式为: ![]() ,
,
当x=6时,y=2,∴点B坐标为 (6,2)
故答案为:![]() 、
、![]() 、(6,2).
、(6,2).
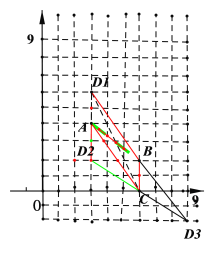
(2)①分别以AB和CD为对角线,AC和BD,AD和BC为
对角线得到如图所示的平行四边形
如图所示,![]() ACBD1,
ACBD1,![]() ABCD2,
ABCD2,![]() ABD3C
ABD3C
②如图所示:D1(3,6)、D2(3,2)、D3(9,-2)


科目:初中数学 来源: 题型:
【题目】有甲、乙两家草莓采摘园,草莓的销售价格相间,在生长旺季,两家均排出优惠方案.甲园的优惠方案是:采摘的草莓不超过![]() 时,按原价销售;若超过
时,按原价销售;若超过![]() 超过部分
超过部分![]() 折优惠;乙园的优惠方案是:游客进园需购买
折优惠;乙园的优惠方案是:游客进园需购买![]() 元门票.采摘的草莓直接按降价出售.已知在甲园、乙园采摘草莓
元门票.采摘的草莓直接按降价出售.已知在甲园、乙园采摘草莓![]() 时,所需费用相同.
时,所需费用相同.
在乙采摘园所需费用![]() ( 元)与草梅采摘量
( 元)与草梅采摘量![]() (千克)满足一次函数关系,如下表:
(千克)满足一次函数关系,如下表:
数量 |
|
|
|
| ··· |
费用 |
|
|
|
| ··· |
(1)求![]() 与
与![]() 的函数关系式(不必写出
的函数关系式(不必写出![]() 的范围);
的范围);
(2)求两个采摘园的草莓在生长旺季前的销售价格.并求在甲采摘园所需费用![]() (元)与草莓采摘量
(元)与草莓采摘量![]() (千克)的函数关系式
(千克)的函数关系式![]() ;
;
(3)若嘉琪准备花费![]() 元去采摘草莓,去哪个园采摘,可以得到更多数量的草莓? 说明理由.
元去采摘草莓,去哪个园采摘,可以得到更多数量的草莓? 说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,创新小组要测量公园内一棵树的高度AB,其中一名小组成员站在距离树10米的点E处,测得树顶A的仰角为54°.已知测角仪的架高CE=1.8米,则这颗树的高度为_________米.(结果保留一位小数.参考数据:sin54°=0.8090,cos54°=0.5878,tan54°=1.3764)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司计划购买A,B两种型号的机器人搬运材料.已知A型机器人比B型机器人每小时多搬运30kg材料,且A型机器人搬运1000kg材料所用的时间与B型机器人搬运800kg材料所用的时间相同.
(1)求A,B两种型号的机器人每小时分别搬运多少材料;
(2)该公司计划采购A,B两种型号的机器人共20台,要求每小时搬运材料不得少于2800kg,则至少购进A型机器人多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016辽宁省葫芦岛市)甲、乙两车从A城出发前往B城,在整个行驶过程中,汽车离开A城的距离y(km)与行驶时间t(h)的函数图象如图所示,下列说法正确的有( )
①甲车的速度为50km/h ②乙车用了3h到达B城
③甲车出发4h时,乙车追上甲车 ④乙车出发后经过1h或3h两车相距50km.

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,点C、点D为⊙O上异于A、B的两点,连接CD,过点C作CE⊥DB,交DB的延长线于点E,连接AC、AD、BC,若∠ABD=2∠BDC.
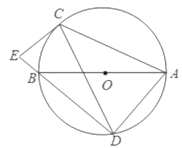
(1)求证:CE是⊙0的切线
(2)求证:△ABC![]() △CBE
△CBE
(3)若⊙O的半径为5,tan∠BDC=![]() ,求BE的长.
,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
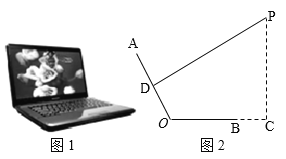
【题目】如图1是一台放置在水平桌面上的笔记本电脑,将其侧面抽象成如图2所示的几何图形.若显示屏AO与键盘BO长均为24cm,点P为眼睛所在位置,D为AO的中点,连接PD,且PD⊥AO(此时点P为最佳视角),点C在OB的延长线上,PC⊥BC,BC=12cm.
(1)当PA=45cm时,求PC的长;
(2)当∠AOC=115°时,线段PC的长比(1)中线段PC的长是增大还是减小?请通过计算说明.(结果精确到0.1cm,sin65°≈0.91,cos65°≈0.42,tan65°≈2.14,sin25°≈0.42,cos25°≈0.91,tan25°≈0.47).
查看答案和解析>>
科目:初中数学 来源: 题型:
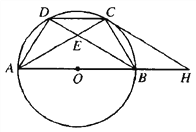
【题目】如图,点A、B、C、D是直径为AB的⊙O上的四个点,CD=BC,AC与BD交于点E。
(1)求证:DC2=CE·AC;
(2)若AE=2EC,求![]() 之值;
之值;
(3)在(2)的条件下,过点C作⊙O的切线,交AB的延长线于点H,若S△ACH=![]() ,求EC之长.
,求EC之长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com