10．数学问题：计算$\frac{1}{m}+\frac{1}{{m}^{2}}+\frac{1}{{m}^{3}}+…+\frac{1}{{m}^{n}}$*（其中m，n都是正整数，且m≥2，n≥1）
探究问题：为解决上面的数字问题，我们运用数形结合的思想方法，通过不断地分割一个面积为1的正方形，把数量关系和几何图形巧妙地结合起来，并采取一般问题特殊化的策略来进行探究．
探究一：计算$\frac{1}{2}+\frac{1}{{2}^{2}}+\frac{1}{{2}^{3}}+…+\frac{1}{{2}^{n}}$
第1次分割，把正方形的面积二等分，其中阴影部分的面积为$\frac{1}{2}$；
第2次分割，把上次分割图中空白部分的面积继续二等分，阴影部分的面积之和为$\frac{1}{2}+\frac{1}{{2}^{2}}$；
第3次分割，把上次分割图中空白部分的面积继续二等分，…；
…
第n次分割，把上次分割图中空白部分的面积最后二等分，所有阴影部分的面积之和为$\frac{1}{2}+\frac{1}{{2}^{2}}+\frac{1}{{2}^{3}}+…+\frac{1}{{2}^{n}}$，最后空白部分的面积是$\frac{1}{{2}^{n}}$．
根据第n次分割图可得等式：$\frac{1}{2}+\frac{1}{{2}^{2}}+\frac{1}{{2}^{3}}+…+\frac{1}{{2}^{n}}$=1-$\frac{1}{{2}^{n}}$．
探究二：计算$\frac{1}{3}$+$\frac{1}{{3}^{2}}+\frac{1}{{3}^{3}}+…+\frac{1}{{3}^{n}}$．
第1次分割，把正方形的面积三等分，其中阴影部分的面积为$\frac{2}{3}$；
第2次分割，把上次分割图中空白部分的面积继续三等分，阴影部分的面积之和为$\frac{2}{3}+\frac{2}{{3}^{2}}$；
第3次分割，把上次分割图中空白部分的面积继续三等分，…；
…
第n次分割，把上次分割图中空白部分的面积最后三等分，所有阴影部分的面积之和为$\frac{2}{3}$+$\frac{2}{{3}^{2}}+\frac{2}{{3}^{3}}+…+\frac{2}{{3}^{n}}$，最后空白部分的面积是$\frac{1}{{3}^{n}}$．
根据第n次分割图可得等式：$\frac{2}{3}$+$\frac{2}{{3}^{2}}+\frac{2}{{3}^{3}}+…+\frac{2}{{3}^{n}}$=1-$\frac{1}{{3}^{n}}$．
两边同除以2，得$\frac{1}{3}$+$\frac{1}{{3}^{2}}+\frac{1}{{3}^{3}}+…+\frac{1}{{3}^{n}}$=$\frac{1}{2}$$-\frac{1}{2×{3}^{n}}$\
探究三：计算$\frac{1}{4}+\frac{1}{{4}^{2}}+\frac{1}{{4}^{3}}+..+\frac{1}{{4}^{n}}$．
（仿照上述方法，只画出第n次分割图，在图上标注阴影部分面积，并写出探究过程）
解决问题：根据前面探究结果：
$\frac{1}{2}+\frac{1}{{2}^{2}}+\frac{1}{{2}^{3}}+…+\frac{1}{{2}^{n}}$=1-$\frac{1}{{2}^{n}}$
$\frac{1}{3}$+$\frac{1}{{3}^{2}}+\frac{1}{{3}^{3}}+…+\frac{1}{{3}^{n}}$=$\frac{1}{2}$$-\frac{1}{2×{3}^{n}}$
$\frac{1}{4}+\frac{1}{{4}^{2}}+\frac{1}{{4}^{3}}+..+\frac{1}{{4}^{n}}$=$\frac{1}{3}$-$\frac{1}{3×{4}^{n}}$．
…
推出：$\frac{1}{m}+\frac{1}{{m}^{2}}+\frac{1}{{m}^{3}}+…+\frac{1}{{m}^{n}}$=$\frac{1}{m-1}$-$\frac{1}{（m-1）{m}^{n}}$．（只填空，其中m、n都是正整数，且m≥2，n≥1）
拓广应用：计算$\frac{5-1}{5}+\frac{{5}^{2}-1}{{5}^{2}}+\frac{{5}^{3}-1}{{5}^{3}}+…+\frac{{5}^{n}-1}{{5}^{n}}$．
如图，在等边三角形ABC中，P是△ABC的一点，PA=1，PB=$\sqrt{7}$，PC=2$\sqrt{2}$，求∠APB的大小． 
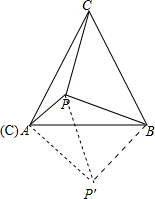解：将△BCP绕B逆时针旋转60°，点C和A重合，P到P′，连接PP′，
考前必练系列答案
如图，在平面直角坐标系xOy中，A（0，3），B（3，0），过B作直线BC⊥x轴，一个动点N自OA的中点M出发，沿直线先到达x轴上的E点，再到直线BC上的F点，最后到达点A．
如图，在△ABC中，AD是∠BAC的外角平分线，P是AD上异于点A的任一点，试比较PB+PC与AB+AC的大小，并说明理由．