
【题目】如图,![]() 是等腰三角形,
是等腰三角形,![]() ,点
,点![]() 是
是![]() 上一点,过点
上一点,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,交
,交![]() 延长线于点
延长线于点![]() .
.
(1)证明:![]() 是等腰三角形;
是等腰三角形;
(2)若![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)见详解 (2)4
【解析】
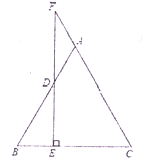
(1)由AB=AC,可知∠B=∠C,再由DE⊥BC,可知∠F+∠C=90°,∠BDE+∠B=90,然后余角的性质可推出∠F=∠BDE,再根据对顶角相等进行等量代换即可推出∠F=∠FDA,于是得到结论;
(2)根据解直角三角形和等边三角形的性质即可得到结论.
证明:(1)∵AB=AC
∴∠B=∠C,
∵FE⊥BC,
∴∠F+∠C=90°,∠BDE+∠B=90°,
∴∠F=∠BDE,
又∵∠BDE=∠FDA,
∴∠F=∠FDA,
∴AF=AD,
∴△ADF是等腰三角形;
(2)∵DE⊥BC,
∴∠DEB=90°,
∵∠B=60°,BD=4,
∴BE=![]() BD=2
BD=2
∵AB=AC
∴△ABC是等边三角形,
∴BC=AB=AD+BD=6,
∴EC=BC-BE=4


科目:初中数学 来源: 题型:
【题目】某校3月份开展网络授课教学,该校随机抽取部分学生,按四个类别(A、很喜欢;B、喜欢;C、一般;D、不喜欢;)统计它们对网络授课的接受情况,并将结果绘制成如下两幅不完整的统计图:
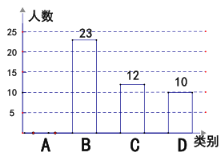
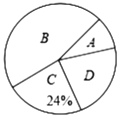
(1)这次共抽取_________名学生进行统计调查;扇形统计图中,D类所对应的扇形圆心角的大小为_______;
(2)将条形图补充完整;
(3)该校共有1500名学生,估计该校表示“喜欢”网络授课的B类的学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
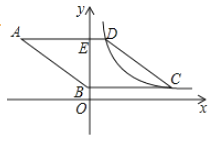
【题目】如图,菱形ABCD的边AD⊥y轴,垂足为点E,顶点A在第二象限,顶点B在y轴的正半轴上,反比例函数y=![]() (k≠0,x>0)的图象同时经过顶点C,D.若点C的横坐标为5,BE=3DE
(k≠0,x>0)的图象同时经过顶点C,D.若点C的横坐标为5,BE=3DE
(1)求出k值.
(2)求出△OCD的面积
(3)试探究坐标轴上是否存在点P,使得△PCD的面积等于菱形ABCD的面积的一半,如果存在,请直接写出点P的坐标;如不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据2019年莆田市初中毕业升学体育考试内容要求,甲、乙、丙在某节体育课他们各自随机分别到篮球场A处进行篮球运球绕杆往返训练或到足球场B处进行足球运球绕杆训练,三名学生随机选择其中的一场地进行训练.
(1)用列表法或树形图表示出的所用可能出现的结果;
(2)求甲、乙、丙三名学生在同一场地进行训练的概率;
(3)求甲、乙、丙三名学生中至少有两人在B处场地进行训练的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列4个结论:①abc<0;②2a+b=0;③4a+2b+c>0;④b2﹣4ac>0;其中正确的结论的个数是( )
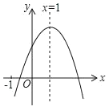
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,对称轴为直线
,对称轴为直线![]() ,
,![]() ,下列结论:①
,下列结论:①![]() ;②9a+3b+c=0;③若点
;②9a+3b+c=0;③若点![]() ,点
,点![]() 是此函数图象上的两点,则
是此函数图象上的两点,则![]() ;④
;④![]() .其中正确的个数( )
.其中正确的个数( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在![]() 中,
中,![]() 为射线
为射线![]() 上一点,连接
上一点,连接![]() 交
交![]() 于点
于点![]() .
.
(1)如图1,若![]() 点与点
点与点![]() 重合,且
重合,且![]() ,求
,求![]() 的长;
的长;
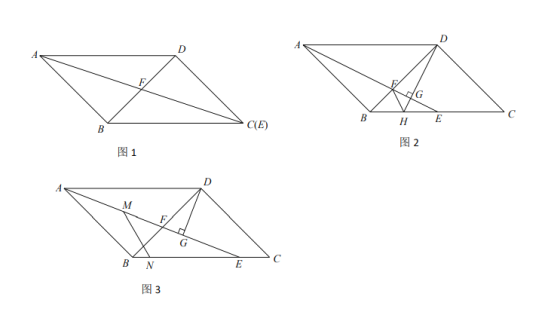
(2)如图2,当点![]() 在
在![]() 边上时,过点
边上时,过点![]() 作
作![]() 于
于![]() ,延长
,延长![]() 交
交![]() 于
于![]() ,连接
,连接![]() .求证:
.求证:![]() .
.
(3)如图3,当点![]() 在射线
在射线![]() 上运动时,过点
上运动时,过点![]() 作
作![]() 于
于![]() 为
为![]() 的中点,点
的中点,点![]() 在
在![]() 边上且
边上且![]() ,已知
,已知![]() ,请直接写出
,请直接写出![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象开口向上,图象经过点(﹣1,2)和(1,0),且与y轴相交于负半轴,给出五个结论:①a+b+c=0,②abc<0,③2a+b>0,④a+c=1,⑤当﹣1<x<1时,y<0;其中正确的结论的序号( )
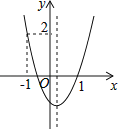
A.①③⑤B.②③④C.①③④D.②③⑤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com