
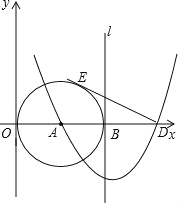
【题目】如图,已知点A(3,0),以A为圆心作⊙A与Y轴切于原点,与x轴的另一个交点为B,过B作⊙A的切线l.
(1)以直线l为对称轴的抛物线过点A及点C(0,9),求此抛物线的解析式;
(2)抛物线与x轴的另一个交点为D,过D作⊙A的切线DE,E为切点,求此切线长;
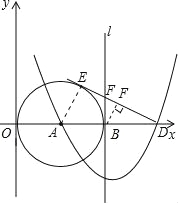
(3)点F是切线DE上的一个动点,当△BFD与△EAD相似时,求出BF的长.
【答案】(1)![]()
(2)![]()
(3)BF的长为![]() 或
或![]() .
.
【解析】
试题分析:(1)已知了抛物线的顶点坐标,可将抛物线的解析式设为顶点坐标式,然后将C点坐标代入求解即可.
(2)由于DE是⊙A的切线,连接AE,那么根据切线的性质知AE⊥DE,在Rt△AED中,AE、AB是圆的半径,即AE=OA=AB=3,而A、D关于抛物线的对称轴对称,即AB=BD=3,由此可得到AD的长,进而可利用勾股定理求得切线DE的长.
(3)若△BFD与EAD△相似,则有两种情况需要考虑:①△AED∽△BFD,②△AED∽△FBD,根据不同的相似三角形所得不同的比例线段即可求得BF的长.
试题解析:(1)设抛物线的解析式为y=a(x﹣6)2+k;
∵抛物线经过点A(3,0)和C(0,9),
∴![]() ,
,
解得:![]() ,
,
∴![]() .
.
(2)连接AE;
∵DE是⊙A的切线,
∴∠AED=90°,AE=3,
∵直线l是抛物线的对称轴,点A,D是抛物线与x轴的交点,
∴AB=BD=3,
∴AD=6;
在Rt△ADE中,DE2=AD2﹣AE2=62﹣32=27,
∴![]() .
.
(3)当BF⊥ED时;
∵∠AED=∠BFD=90°,∠ADE=∠BDF,
∴△AED∽△BFD,
∴![]() ,
,
即![]() ,
,
∴![]() ;
;
当FB⊥AD时,
∵∠AED=∠FBD=90°,∠ADE=∠FDB,
∴△AED∽△FBD,
∴![]() ,
,
即![]() ;
;
∴BF的长为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】我们用有理数的运算研究下面问题.规定:水位上升为正,水位下降为负;几天后为正,几天前为负.如果水位每天下降4cm,那么3天后的水位变化用算式表示正确的是( )
A. (+4)×(+3) B. (+4)×(﹣3) C. (﹣4)×(+3) D. (﹣4)×(﹣3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数y=![]() (m为常数)的图象在一、三象限.
(m为常数)的图象在一、三象限.
(1)求m的取值范围;
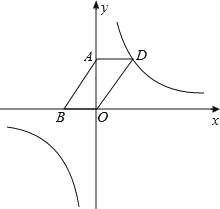
(2)如图,若该反比例函数的图象经过ABOD的顶点D,点A、B的坐标分别为(0,3),(﹣2,0).
①求出函数解析式;
②设点P是该反比例函数图象上的一点,若OD=OP,则P点的坐标为 ;若以D、O、P为顶点的三角形是等腰三角形,则满足条件的点P的个数为 个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】AD是△ABC的角平分线且交BC于D,过点D作DE⊥AB于E,DF⊥AC于F,则下列结论不一定正确的是( )
A.DE=DF B.BD =CD C.AE=AF D.∠ADE=∠ADF
查看答案和解析>>
科目:初中数学 来源: 题型:
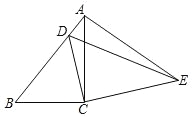
【题目】如图,在△ABC中,∠ACB=90°,AB=9,cosB=![]() ,把△ABC绕着点C旋转,使点B与AB边上的点D重合,点A落在点E,则点A、E之间的距离为 .
,把△ABC绕着点C旋转,使点B与AB边上的点D重合,点A落在点E,则点A、E之间的距离为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,D是斜边AB上的中点,E是边BC上的点,AE与CD交于点F,且AC2=CECB.
(1)求证:AE⊥CD;
(2)连接BF,如果点E是BC中点,求证:∠EBF=∠EAB.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com