
����Ŀ����̽�����֡�
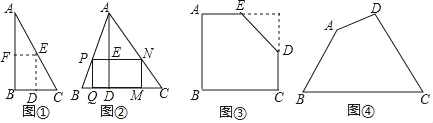
��ͼ������һ��ֱ��������ֽƬ����B=90����С������м���һ������BΪ�ڽ���������ľ��Σ�������β������֣���������λ��DE��EF����ʱ�����õľ��ε������������ͨ��֤����֤������ȷ�ԣ����ó������ε���������ԭ����������ı�ֵΪ�� ����
����չӦ�á�
��ͼ��������ABC�У�BC=a��BC���ϵĸ�AD=h������PQMN�Ķ���P��N�ֱ��ڱ�AB��AC�ϣ�����Q��M�ڱ�BC�ϣ������PQMN��������ֵΪ�� �������ú�a��h�Ĵ���ʽ��ʾ��
�����Ӧ�á�
��ͼ������һ����ȱ�Ǿ�����ABCDE��AB=32��BC=40��AE=20��CD=16��С�����м�����һ��������ľ��Σ���BΪ���������ε��ڽǣ�����þ��ε������
��ʵ��Ӧ�á�
��ͼ��������һ���ı��ε�ľ������ABCD��������AB=50cm��BC=108cm��CD=60cm����tanB=tanC=![]() ��ľ����ʦ������������вó��˶���M��N�ڱ�BC����������ľ���PQMN����þ��ε������
��ľ����ʦ������������вó��˶���M��N�ڱ�BC����������ľ���PQMN����þ��ε������
���𰸡��������.
��������������������̽�����֡�������λ��֪EF=![]() BC��ED=
BC��ED=![]() AB����
AB���� �ɵã�
�ɵã�
����չӦ�á�������APN�ס�ABC֪![]() ���ɵ�PN=a-
���ɵ�PN=a-![]() PQ����PQ=x����S����PQMN=PQPN�T-
PQ����PQ=x����S����PQMN=PQPN�T-![]() ��x-
��x-![]() ��2+
��2+![]() ���ݴ˿ɵã�
���ݴ˿ɵã�
�����Ӧ�á���������ͼ1�����ߣ�ȡBF�е�I��FG���е�K���ɾ�������֪AE=EH=20��CD=DH=16���ֱ�֤��AEF�ա�HED����CDG�ա�HDE��AF=DH=16��CG=HE=20���Ӷ��жϳ���λ��IK�����˵����߶�AB��DE�ϣ����á�̽�����֡����۽�ɣ�
��ʵ��Ӧ�á����ӳ�BA��CD���ڵ�E������E��EH��BC�ڵ�H����tanB=tanC֪EB=EC��BH=CH=54��EH=![]() BH=72���̶����BE=CE=90�����ж���λ��PQ�����˵����߶�AB��CD�ϣ����á���չӦ�á����۽��ɵã�
BH=72���̶����BE=CE=90�����ж���λ��PQ�����˵����߶�AB��CD�ϣ����á���չӦ�á����۽��ɵã�
�����������̽�����֡�
��EF��EDΪ��ABC��λ�ߣ�
��ED��AB��EF��BC��EF=![]() BC��ED=
BC��ED=![]() AB��
AB��
�֡�B=90����
���ı���FEDB�Ǿ��Σ�
��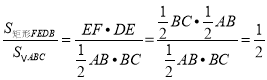 ��
��
����չӦ�á�
��PN��BC��
���APN�ס�ABC��
��![]() ����
����![]() ��
��
��PN=a-![]() PQ��
PQ��
��PQ=x��
��S����PQMN=PQPN=x��a-![]() x��=-
x��=-![]() x2+ax=-
x2+ax=-![]() ��x-
��x-![]() ��2+
��2+![]() ��
��
�൱PQ=![]() ʱ��S����PQMN���ֵΪ
ʱ��S����PQMN���ֵΪ![]() .
.
�����Ӧ�á�
��ͼ1���ӳ�BA��DE���ڵ�F���ӳ�BC��ED���ڵ�G���ӳ�AE��CD���ڵ�H��ȡBF�е�I��FG���е�K��

������֪�ı���ABCH�Ǿ��Σ�
��AB=32��BC=40��AE=20��CD=16��
��EH=20��DH=16��
��AE=EH��CD=DH��
����AEF����HED��
�� ��
��
���AEF�ա�HED��ASA����
��AF=DH=16��
ͬ����CDG�ա�HDE��
��CG=HE=20��
��BI=![]() =24��
=24��
��BI=24��32��
����λ��IK�����˵����߶�AB��DE�ϣ�
����K��KL��BC�ڵ�L��
�ɡ�̽�����֡�֪���ε�������Ϊ![]() ��BG
��BG![]() BF=
BF=![]() ����40+20����
����40+20����![]() ��32+16��=720��
��32+16��=720��
�𣺸þ��ε����Ϊ720��
��ʵ��Ӧ�á�

��ͼ2���ӳ�BA��CD���ڵ�E������E��EH��BC�ڵ�H��
��tanB=tanC=![]() ��
��
���B=��C��
��EB=EC��
��BC=108cm����EH��BC��
��BH=CH=![]() BC=54cm��
BC=54cm��
��tanB=![]() =
=![]() ��
��
��EH=![]() BH=
BH=![]() ��54=72cm��
��54=72cm��
��Rt��BHE��BE=![]() =90cm��
=90cm��
��AB=50cm��
��AE=40cm��
��BE���е�Q���߶�AB�ϣ�
��CD=60cm��
��ED=30cm��
��CE���е�P���߶�CD�ϣ�
����λ��PQ�����˵����߶�AB��CD�ϣ�
�ɡ���չӦ�á�֪������PQMN��������Ϊ![]() BCEH=1944cm2��
BCEH=1944cm2��
�𣺸þ��ε����Ϊ1944cm2��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
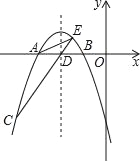
����Ŀ����ͼ��������y=��![]() x2+bx+c��x����A��B���㣬��������C����֪��A�������ǣ���6��0������C�������ǣ���8����6����
x2+bx+c��x����A��B���㣬��������C����֪��A�������ǣ���6��0������C�������ǣ���8����6����
��1���������ߵĽ���ʽ��
��2���������ߵĶ������꼰��B�����ꣻ
��3���������ߵĶԳ�����x�ύ�ڵ�D������CD�����ӳ�CD���������ڵ�E������AC��AE������ACE�������
��4������������һ������M����A��B���㹹����ABM���Ƿ����S��ADM=![]() S��ACD�������ڣ��������M�����ꣻ�������ڣ���˵�����ɣ�
S��ACD�������ڣ��������M�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�AD��80cm��AB��40cm���뾶Ϊ8cm�ġ�O�ھ���������AB��AD�����У����ж���P��A��������ھ��α�������A��B��C��D�ķ��������ƶ�������P����D��ʱֹͣ�ƶ�����O�ھ����ڲ���AD��������ƽ�ƣ��ƶ�����CD����ʱ������ԭ·��ԭ�ٷ��أ�����O�ص�����ʱ��λ�ã����ٴ���AB���У�ʱֹͣ�ƶ�����֪��P���Oͬʱ��ʼ�ƶ���ͬʱֹͣ�ƶ�����ͬʱ������Ե���ֹλ�ã�������O�����O1��λ��ʱ����ʱԲ��O1�ھ��ζԽ���BD�ϣ���DP���O1ǡ�����У���ʱ��O�ƶ��ˣ�������cm��
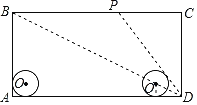
A.56B.72C.56��72D.������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�ı߳�Ϊ4����E�Խ���BD�ϣ��ҡ�BAE=22.5����EF��AB������Ϊ��F����EF�ij�Ϊ�� ��
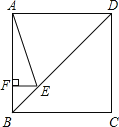
A. 1B. 4-![]() C.
C. ![]() D.
D. ![]() -4
-4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��a�����ĸ�������b����С������������c��a+b����ش��������⣺
![]()
��1����ֱ��д��a��b��c��ֵ��a���� ����b���� ����c���� ����
��2��a��b��c������������Ӧ�ĵ�ֱ�ΪA��B��C��������ͼ�������ϱ�ʾ��A��B��C���㣻
��3���ڣ�2��������£���A��B��C��ʼ���������˶�������A����C��ÿ��1����λ���ٶ������˶���ͬʱ����B��ÿ��5����λ���ȵ��ٶ������˶�������t���ӹ�������B���C֮��ľ����ʾΪBC����A���B֮��ľ����ʾΪAB�����ʣ�AB��BC��ֵ�Ƿ�����ʱ��ı仯���ı䣿���仯����˵�����ɣ������䣬�����AB��BC��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˱���������㴫ͳ�Ļ���ijУ��֯��һ�Ρ�ʫ�ʴ�ᡱ��С����С��ͬʱ�μӣ����У���һ���ش����ǣ�����ͼ��ʾ�ľŹ�����ѡȡ�߸������һ����ʫ�����Ϊ��ɽ��ˮ������·����
��1��С���ش������ʱ���Եڶ�������ѡ���ء�����ѡ������Ծ��������ѡ������һ������С���ش���ȷ�ĸ����� ��
��2��С���ش������ʱ���Եڶ�������ѡ���ء�����ѡ��������ĸ�����ѡ����������ѡ�����������Ծ������ֱ����ѡ�������б�����״ͼ�ķ�����С���ش���ȷ�ĸ��ʣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����D��E�ֱ��ǡ�ABC��BC��AC�ߵ��е�.
(1)��ͼ�٣���AB=10����DE�ij���
(2)��ͼ��,��F��AB���ϵ�һ��,FG//AD,��ED���ӳ����ڵ�G.��֤��AF=DG
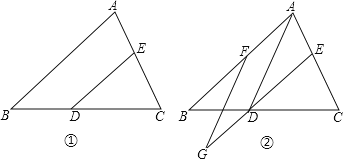
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С������Ҫ�øֹ����������������Ҫ��������Ҫ��Ϊ 0.8m��2.5m �Ҵ�ϸ��ͬ�ĸֱֹܷ�Ϊ 100 ����32 ������Ҫ����Щ���ϲ����Ǻ��Ӷ��ɵģ��ֲָ��г������ֹ��ĸֹ�ÿ��Ϊ 6m��
��1������һ�� 6m ����Բ�ֹ�����Щ�ü������أ�����д�¿գ��������ϣ���
�����٣���ֻ�ü���Ϊ 0.8m ������ʱ�����ɼ� ����
�����ڣ����ȼ��� 1 �� 2.5m ������ʱ�����²�������ܼ� 0.8m �������� ����
�����ۣ����ȼ��� 2 �� 2.5m ������ʱ�����²�������ܼ� 0.8m �������� ����
��2���ֱ��ã�1���еķ����ںͷ����۸��ü����ٸ� 6m ���ĸֹܣ����ܸպõõ�����Ҫ����Ӧ�����IJ��ϣ�
��3����̽��������2���з����⣬�ڣ�1���л��������ַ������ϣ�����Ҫ 6m ���ĸֹ��루2�� �и�����ͬ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ij��������A��B�����й�·����·��������ҹ�����A�ع���һ��ÿ��1000Ԫ��ԭ���˻ع������Ƴ�ÿ��8000Ԫ�IJ�Ʒ�˵�B�أ���֪��·�˼�Ϊ1.4Ԫ/����ǧ�ף�����·�˼�Ϊ1.1Ԫ/����ǧ�ף��������������乲֧����·�����14000Ԫ����·�����89100Ԫ����
��1���ù�����A�ع����˶��ٶ�ԭ�ϣ��Ƴ�����B�صIJ�Ʒ���ٶ֣�
��2��������Ʒ�����ۿ��ԭ�Ϸ�������ѵĺͶ����Ԫ��

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com