
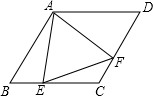
 如图所示,在菱形ABCD中,E、F分别是BC、CD上的点,且∠B=∠EAF=60°,∠BAE=24°,求∠CEF的度数.
如图所示,在菱形ABCD中,E、F分别是BC、CD上的点,且∠B=∠EAF=60°,∠BAE=24°,求∠CEF的度数. 分析 先连接AC,证明△ABE≌△ACF,然后推出AE=AF,证明△AEF是等边三角形,最后运用三角形外角性质,求出∠CEF的度数.
解答 解:连接AC,
∵四边形ABCD是菱形,
∴AB=BC=CD=AD,
∵∠B=∠EAF=60°,
∴△ABC是等边三角形,∠BCD=120°,
∴AB=AC,∠B=∠ACF=60°,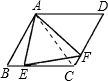
∵∠BAE+∠EAC=∠FAC+∠EAC,
∴∠BAE=∠FAC,
在△ABE与△ACF中,
$\left\{\begin{array}{l}{∠BAE=∠CAF}\\{AB=AC}\\{∠B=∠ACF}\end{array}\right.$,
∴△ABE≌△ACF(ASA),
∴AE=AF,
又∵∠EAF=∠D=60°,
∴△AEF是等边三角形,
∴∠AEF=60°,
又∠AEC=∠B+∠BAE=84°,
∴∠CEF=84°-60°=24°.
点评 此题主要考查菱形的性质、等边三角形的判定以及三角形的内角和定理的综合应用,解答本题的关键是正确作出辅助线,构造全等三角形.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
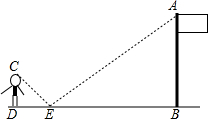 如图,在点E处水平放置一面镜子,人站在D处,恰好能看见旗杆的顶端A,测量眼睛C距地面的高度CD=1.65m,且人与镜子和旗杆底端的距离分别为DE=2m,DB=14.8m.请你计算出旗杆的高度.
如图,在点E处水平放置一面镜子,人站在D处,恰好能看见旗杆的顶端A,测量眼睛C距地面的高度CD=1.65m,且人与镜子和旗杆底端的距离分别为DE=2m,DB=14.8m.请你计算出旗杆的高度.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
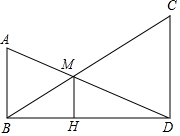 如图,AB和CD表示两根立于地面的柱子,AD和BC表示起固定作用的两根钢筋,AD与BC的交点为M.已知AB=10m,CD=15m,则点M离地面的高度MH=6m.
如图,AB和CD表示两根立于地面的柱子,AD和BC表示起固定作用的两根钢筋,AD与BC的交点为M.已知AB=10m,CD=15m,则点M离地面的高度MH=6m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com