练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    4．已知x+y=$\sqrt{3}$，xy=$\sqrt{6}$，则x2y+xy2的值为3$\sqrt{2}$．

    分析 根据x+y=$\sqrt{3}$，xy=$\sqrt{6}$，可以求得x2y+xy2的值．

    解答 解：∵x+y=$\sqrt{3}$，xy=$\sqrt{6}$，
    ∴x2y+xy2
    =xy（x+y）
    =$\sqrt{6}×\sqrt{3}$
    =$\sqrt{18}$
    =3$\sqrt{2}$，
    故答案为：$3\sqrt{2}$．

    点评 本题考查因式分解的应用，解答本题的关键是明确因式分解的方法，利用题目中的已知条件解答．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

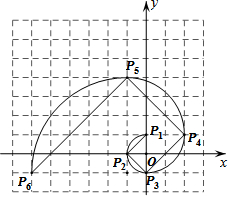    14．我们把1，1，2，3，5，8，13，21，…这组数称为斐波那契数列，为了进一步研究，依次以这列数为半径作90°圆弧$\widehat{{P_1}{P_2}}$，$\widehat{{P_2}{P_3}}$，$\widehat{{P_3}{P_4}}$，…得到斐波那契螺旋线，然后顺次连结P1P2，P2P3，P3P4，…得到螺旋折线（如图），已知点P1（0，1），P2（-1，0），P3（0，-1），则该折线上的点P9的坐标为（　　）
    A．（-6，24）B．（-6，25）C．（-5，24）D．（-5，25）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．小明所在的学校加强学生的体育锻炼，准备从某体育用品商店一次购买若干个足球和篮球（每个足球的价格相同，每个篮球的价格相同），若购买2个篮球和3个足球共需310元，购买5个篮球和2个足球共需500元．
    （1）每个篮球和足球各需多少元？
    （2）根据实际情况，需从该商店一次性购买篮球和足球功60个，要求购买篮球和足球的总费用不超过4000元，那么最多可以购买多少个篮球？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

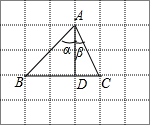    12．△ABC在网格中的位置如图所示（每个小正方形边长为1），AD⊥BC于D，下列四个选项中，错误的是（　　）
    A．sinα=cosαB．tanC=2C．sinβ=cosβD．tanα=1

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    19．如图，把正方形铁片OABC置于平面直角坐标系中，顶点A的坐标为（3，0），点P（1，2）在正方形铁片上，将正方形铁片绕其右下角的顶点按顺时针方向依次旋转90°，第一次旋转至图①位置，第二次旋转至图②位置…，则正方形铁片连续旋转2017次后，点P的坐标为（6053，2）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．一件商品的进价为80元，七折售出仍可获利5%．若标价为x元，则可列方程为（　　）
    A．80（1+5%）=0.7xB．80×0.7（1+5%）=xC．（1+5%）x=0.7xD．80×5%=0.7x

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

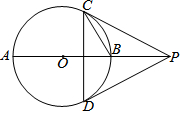    16．如图，AB是⊙O的直径，弦CD⊥AB，过点C作⊙O的切线与AB的延长线交于点P．若∠BCD=32°，则∠CPD的度数是（　　）
    A．64°B．62°C．58°D．52°

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．如图，方格纸中每个小正方形的边长均为1，线段AB的两个端点均在小正方形的顶点上．
    （1）在图中画出以AB为底、面积为12的等腰△ABC，且点C在小正方形的顶点上；
    （2）在图中画出平行四边形ABDE，且点D和点E均在小正方形的顶点上，tan∠EAB=$\frac{3}{2}$，连接CD，请直接写出线段CD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．解不等式组：$\left\{\begin{array}{l}{2x-3＞1}\\{\frac{2-x}{3}＞\frac{x}{3}-2}\end{array}\right.$．

    查看答案和解析>>

    同步练习册答案