
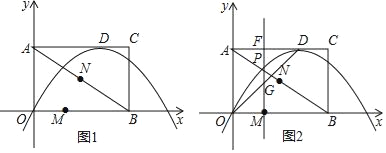
【题目】如图所示,在平面直角坐标系中,矩形AOBC的两边与坐标轴重合,且OB=4,AO=3,若AD=3DC,以D为顶点的抛物线过原点.点M、N为动点,设运动时间为t秒.
(1)求抛物线的解析式;
(2)在图1中,若点M在线段OB上从点O向点B以1个单位/秒的速度运动,同时,点N在线段BA上从点B向点A以2个单位/秒的速度运动,当一个点到达终点时,另一个点随之停止运动.当t为何值时,△BMN为直角三角形?
(3)在图2中,过点M做y轴的平行线,分别交抛物线和线段OD于P、G两点,当t为何值时,△ODP的面积最大?最大值是多少?
【答案】(1)y=﹣![]() x2+2x;(2)当t=
x2+2x;(2)当t=![]() 或t=
或t=![]() 时,△BMN为直角三角形;(3)当t=
时,△BMN为直角三角形;(3)当t=![]() 时,△OPD的面积最大,最大值为
时,△OPD的面积最大,最大值为![]()
【解析】分析:(1)求出点D的坐标,再利用顶点坐标式求出抛物线的解析式;
(2)分∠NMB=90°时,△AOB∽△NMB和当∠MNB=90°时,得到△AOB∽△MNB两种情况进行讨论,求出t的值即可;
(3)首先求出直线OD的解析式,再用t表示出PG的长,用t表示出△OPD的面积,进而求出最大值.
详解:(1)由题意,知AC=4,AD=3CD,得D点坐标为(3,3),根据顶点式设抛物线的解析式为y=a(x﹣3)2+3,
将点O坐标代入即可求出a=﹣![]() ,
,
∴抛物线的解析式为y=﹣![]() x2+2x;
x2+2x;
(2)依题意得,OA=3,OB=4,
∴AB=5,
∵OM=t,故得BM=(4﹣t),BN=2t,
①当∠NMB=90°时,得到△AOB∽△NMB,
得到![]() =
=![]() ,得
,得![]() =
=![]() ,解得t=
,解得t=![]() ;
;
②当∠MNB=90°时,得到△AOB∽△MNB,
得![]() =
=![]() ,得
,得![]() =
=![]() ,解得t=
,解得t=![]() ,
,
∴当t=![]() 或t=
或t=![]() 时,△BMN为直角三角形;
时,△BMN为直角三角形;
(3)∵O(0,0),D(3,3),
∴设直线OD的解析式为y=kx,则3k=3,k=1,
故直线OD的解析式为y=x,
∵OM=t,故xM=xG=xF=t,
∴yP=﹣![]() t2+2t,yG=t,
t2+2t,yG=t,
∴PG=﹣![]() t2+t,
t2+t,
∴S△OPD=![]() ADFG=﹣
ADFG=﹣![]() t2+
t2+![]() t,
t,
∴S△OPD=![]() (t﹣
(t﹣![]() )2+
)2+![]() (0<t<
(0<t<![]() ),
),
∴当t=![]() 时,△OPD的面积最大,最大值为
时,△OPD的面积最大,最大值为![]() .
.


 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:
【题目】粮库6天内粮食进出库的吨数如下(“+”表示进库“-”表示出库)
+25, +8,-12,+34,-36,-22.
(1)经过这6天,粮库里的粮食是增多还是减少了?通过计算说明.
(2)经过这6天,仓库管理员结算发现库里还存480吨粮,那么6天前库里存粮多少吨?
(3)如果进出的装卸费都是每吨5元,那么这6天要付多少装卸费?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着人们生活水平的提高,家用轿车越来越多地进入家庭.小明家中买了一辆小轿车,他连续记录了7天中每天行驶的路程(如表),以50km为标准,多于50km的记为“+”,不足50km的记为“﹣”,刚好50km的记为“0”.
第一天 | 第二天 | 第三天 | 第四天 | 第五天 | 第六天 | 第七天 | |
路程(km) | ﹣8 | ﹣11 | ﹣14 | 0 | ﹣16 | +41 | +8 |
(1)请求出这七天平均每天行驶多少千米;
(2)若每行驶100km需用汽油6升,汽油价6.2元/升,请估计小明家一个月(按30天计)的汽油费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,点A(0,4),C(2,0).

(1)三角形![]() 的面积= ;
的面积= ;
(2)已知坐标轴上有两动点P、Q同时出发,P点从C点出发沿![]() 轴负方向以1个单位长度每秒的速度匀速移动,Q点从O点出发以2个单位长度每秒的速度沿
轴负方向以1个单位长度每秒的速度匀速移动,Q点从O点出发以2个单位长度每秒的速度沿![]() 轴正方向移动,点Q到达A点整个运动随之结束,AC的中点D的坐标是(1,2),设运动时间为
轴正方向移动,点Q到达A点整个运动随之结束,AC的中点D的坐标是(1,2),设运动时间为![]() 秒,问:是否存在这样的
秒,问:是否存在这样的![]() ,使
,使![]() 若存在,请求出的值;若不存在,请说明理由;
若存在,请求出的值;若不存在,请说明理由;
(3)如图2,点F是线段AC上一点,满足∠FOC=∠FCO,点G是第二象限中一点,连OG,使得∠AOG=∠AOF,点E是线段OA上一动点,连CE交OF于点H,当点E在线段OA上运动的过程中,以下两个式子:![]() 哪个式子为定值,请求出这个定值.
哪个式子为定值,请求出这个定值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一种蔬菜![]() 千克,不加工直接出售每千克可卖
千克,不加工直接出售每千克可卖![]() 元;如果经过加工重量减少了20%,价格增加了40%,问:
元;如果经过加工重量减少了20%,价格增加了40%,问:
(1)![]() 千克这种蔬菜加工后可卖多少钱;
千克这种蔬菜加工后可卖多少钱;
(2)如果这种蔬菜1000千克,加工后出售一共可卖2576元,问1000千克这种蔬菜不加工直接出售每千克可卖多少钱?1000千克这种蔬菜加工后出售比不加工直接出售一共多卖多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的大致图象如图所示,关于该二次函数,下列说法中错误的是( )
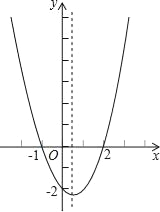
A. 函数有最小值 B. 对称轴是直线x=![]()
C. 当﹣1<x<2时,y<0 D. 当x>![]() 时,y随x的增大而增大
时,y随x的增大而增大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班同学响应“阳光体育运动”号召,利用课外活动积极参加体育锻炼,每位同学从长跑、铅球、立定跳远、篮球定点投篮中任选一项进行了训练,训练前后都进行了测试,现将项目选择情况及训练后篮球定点投篮进球数进行整理,作出如下统计图表.
训练后篮球定点投篮测试进球统计表:
进球数(个) | 8 | 7 | 6 | 5 | 4 | 3 |
人数 | 2 | 1 | 4 | 7 | 8 | 2 |
(1)选择长跑训练的人数占全班人数的百分比是 ,该班共有同学 人.
(2)求训练后篮球定点投篮人均进球数为多少个?
(3)根据测试资料,参加篮球定点投篮的学生训练后比训练前的人均进球增加了25%,求参加训练之前的人均进球数.

查看答案和解析>>
科目:初中数学 来源: 题型:
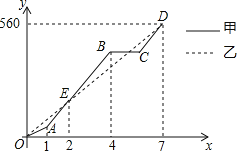
【题目】端午节期间,甲、乙两人沿同一路线行驶,各自开车同时去离家560千米的景区游玩,甲先以每小时60千米的速度匀速行驶1小时,再以每小时m千米的速度匀速行驶,途中体息了一段时间后,仍按照每小时m千米的速度匀速行驶,两人同时到达目的地,图中折线、线段分别表示甲、乙两人所走的路程![]() ,
,![]() 与时间
与时间![]() 之间的函数关系的图象
之间的函数关系的图象![]() 请根据图象提供的信息,解决下列问题:
请根据图象提供的信息,解决下列问题:
![]() 图中E点的坐标是______,题中
图中E点的坐标是______,题中![]() ______
______![]() ,甲在途中休息______h;
,甲在途中休息______h;
![]() 求线段CD的解析式,并写出自变量x的取值范围;
求线段CD的解析式,并写出自变量x的取值范围;
![]() 两人第二次相遇后,又经过多长时间两人相距20km?
两人第二次相遇后,又经过多长时间两人相距20km?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】肥西素有“淮军故里、改革首县、花木之乡”之美誉,现就肥西以下五个旅游景点进行调查,A.“官亭林海”,B.“三河古镇”,C.“紫蓬山国家森林公园”,D.“小井庄”,E.“刘铭传故居”,为了解学生最喜欢哪一个景点(每人只选取一种),随机抽取了部分学生进行调查,将调查结果绘制成如下不完整的统计表和统计图.根据以上信息解答下列问题:


(1)本次接受调查的总人数为______人,统计表中m=______,n=______.
(2)补全条形统计图.
(3)若把条形统计图改为扇形统计图,则景点“紫蓬山国家森林公园”、“小井庄”、“刘铭传故居”所在扇形的圆心角度数分别是__________、___________、___________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com