
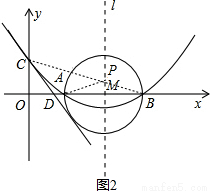
如图,已知抛物线的对称轴为直线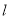 :
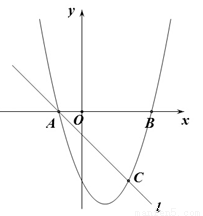
: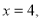 且与
且与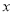 轴交于点
轴交于点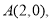 与
与 轴交于点
轴交于点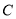
 .
.
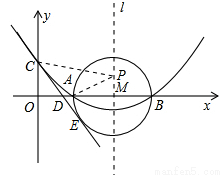
(1)求抛物线的解析式;
(2)试探究在此抛物线的对称轴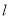 上是否存在一点
上是否存在一点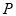 ,使
,使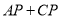 的值最小?若存在,求
的值最小?若存在,求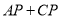 的最小值,若不存在,请说明理由;
的最小值,若不存在,请说明理由;
(3)以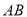 为直径作⊙
为直径作⊙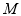 ,过点
,过点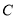 作直线
作直线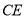 与⊙
与⊙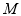 相切于点
相切于点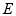 ,
,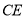 交
交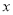 轴于点
轴于点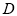 ,求直线
,求直线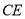 的解析式.
的解析式.
【解析】
(1)如图,由题意,设抛物线的解析式为:
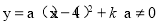
∵抛物线经过 、
、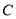
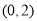 .
.
∴
解得:a=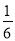 ,
,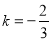 .
.
∴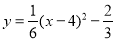 ,
,
即: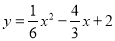 .
.
(2)存在.
令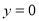 , 得
, 得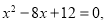
即 ,
,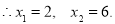
 抛物线与
抛物线与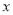 轴的另-交点
轴的另-交点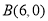 .
.
如本题图2,连接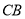 交
交 于点
于点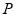 ,则点
,则点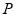 即是使
即是使 的值最小的点.
的值最小的点.
 因为
因为 关于
关于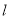 对称,则
对称,则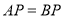 ,
, ,即
,即 的最小值为
的最小值为 .
.
∵ ,
,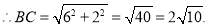
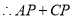 的最小值为
的最小值为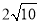 ;
;
(3)如图3,连接 ,∵
,∵ 是⊙
是⊙ 的切线,
的切线,

∴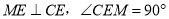 ,
,
由题意,得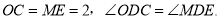
∵在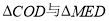 中,
中,
 ,
,
∴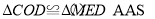 ,
,
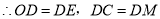 ,
,
设 ,则
,则 ,
,
则在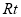 △
△ 中,又
中,又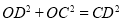 ,
,
∴ ,解得
,解得 ,
,
∴ (
(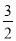 ,0)
,0)
设直线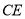 的解析式为
的解析式为 ,∵直线
,∵直线 过
过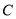 (0,2)、
(0,2)、 (
(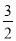 ,0)两点,
,0)两点,

 ,解方程组得:
,解方程组得: .
.
∴直线 的解析式为
的解析式为
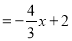 .
.
【解析】
试题分析:(1)根据题意设抛物线的解析式为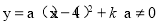 ,将
,将 、
、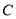
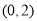 代入解析式,即可求出a,k的值,得出抛物线的解析式,令
代入解析式,即可求出a,k的值,得出抛物线的解析式,令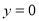 ,即可求出抛物线与
,即可求出抛物线与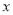 轴另-交点
轴另-交点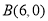 ;(2)连接
;(2)连接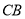 交
交 于点
于点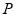 ,则点
,则点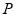 即是使
即是使 的值最小的点. 则
的值最小的点. 则 的最小值为
的最小值为 ,在Rt△OBC中,根据勾股定理即可求出BC的值;(3)连接
,在Rt△OBC中,根据勾股定理即可求出BC的值;(3)连接 ,根据已知条件可得
,根据已知条件可得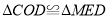 ,根据全等三角形的对应边相等可得
,根据全等三角形的对应边相等可得 ,在
,在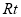 △
△ 中,根据勾股定理求出OD,即可得出D点坐标,设直线
中,根据勾股定理求出OD,即可得出D点坐标,设直线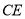 的解析式为
的解析式为 ,代入C,D两点坐标,即可解得直线
,代入C,D两点坐标,即可解得直线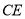 的解析式.
的解析式.
考点:二次函数的综合题.


科目:初中数学 来源:2014-2015学年山东省临沂市九年级上学期基础学科竞赛数学试卷(解析版) 题型:解答题
(本小题满分10分)如图,抛物线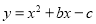 与
与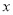 轴交
轴交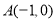 、
、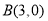 两点,直线
两点,直线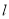 与抛物线交于A、C两点,其中C点的横坐标为2.
与抛物线交于A、C两点,其中C点的横坐标为2.
(1)求抛物线及直线AC的函数表达式;
(2)若P点是线段AC上的一个动点,过P点作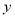 轴的平行线交抛物线于F点,求线段PF长度的最大值.
轴的平行线交抛物线于F点,求线段PF长度的最大值.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省临沂市九年级上学期基础学科竞赛数学试卷(解析版) 题型:选择题
如图,小明想用图中所示的扇形纸片围成一个圆锥,已知扇形的半径为5cm,弧长是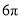 cm,那么围成的圆锥的高度是
cm,那么围成的圆锥的高度是
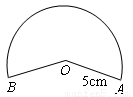
A.3㎝ B.4㎝ C.5 ㎝ D.6㎝
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省临沂市九年级上学期基础学科竞赛数学试卷(解析版) 题型:选择题
如图,△ABC中,点D在线段BC上,且△ABC∽△DBA,则下列结论一定正确的是
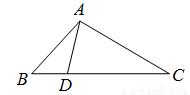
A.AB2=BC·BD B.AB2=AC·BD
C.AB·AD=BD·BC D.AB·AD=AD ·CD
查看答案和解析>>
科目:初中数学 来源:2014-2015学年广东省广州市番禺区九年级上学期期末模拟质量抽测数学试卷(解析版) 题型:解答题
已知二次函数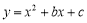 的图象过点(4,3)、(3,0).
的图象过点(4,3)、(3,0).
(1)求 、
、 的值;
的值;
(2)求出该二次函数图象的顶点坐标和对称轴;
(3)在下图中作出此二次函数的图象,根据图像说明,当 取何值时,
取何值时, ?
?

查看答案和解析>>
科目:初中数学 来源:2014-2015学年广东省东莞市八年级上学期期末考试数学试卷(解析版) 题型:解答题
某工厂现在平均每天比原计划多生产20台机器,现在生产300台机器所需时间与原计划生产150台机器所需时间相同,求现在平均每天生产多少台机器.
查看答案和解析>>
科目:初中数学 来源:[同步]2014年华师大版八年级上 13.5逆命题与逆定理练习卷(解析版) 题型:?????
用反证法证明“a>b”时应假设( )
A.a>b B.a<b C.a=b D.a≤b
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com