
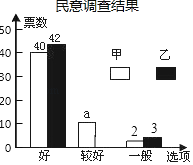
【题目】我校2019年度“一中好声音“校园歌手比赛已正式拉开序幕,其中甲,乙两位同学的表现分外突出,现场A、B、C、D、E、F六位评委的打分情况以及随机抽取的50名同学的民意调查结果分别如下统计表和不完整的条形统计图:
A | B | C | D | E | F | |
甲 | 88 | m | 90 | 93 | 95 | 96 |
乙 | 89 | 92 | 90 | 97 | 94 | 93 |
(1)a= ,六位评委对乙同学所打分数的中位数是 ,并补全条形统计图;
(2)六位评委对甲同学所打分数的平均分为92分,则m= ;
(3)学校规定评分标准:去掉评委评分中最高和最低分,再算平均分,并将平均分与民意测评分按3:2计算最后得分,求甲、乙两位同学的得分,(民意测评分=“好”票数×2+“较好”票数×1+“一般”票数×0)
(4)现准备从甲、乙两位同学中选一位优秀同学代表重庆一中参加市歌手大赛,请问选哪位同学?并说明理由.
【答案】(1)8,92.5,见解析;(2)90;(3)90.4,90.95;(4)选乙,理由见解析
【解析】
(1)利用50减去甲同学“好”的票数和“一般”的票数即可求出a,根据中位数的定义计算即可,求出乙同学“较好”的票数,然后补全条形统计图;
(2)根据平均数公式列出方程即可求出结论;
(3)先求出评委评分中,甲、乙的平均分,然后根据题意即可求出结论;
(4)比较(3)中两人的分数即可得出结论.
解:(1)a=50﹣40﹣2=8,
六位评委对乙同学所打分数的中位数是![]() =
=![]() .
.
故答案为8,92.5.
乙同学较好的有50﹣42﹣3=5(票),条形图如图所示
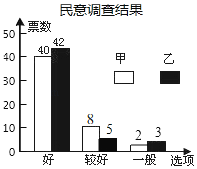 :
:
(2)由题意92=![]() ,
,
解得m=90,
故答案为90.
(3)评委评分中,甲的平均分为![]() ,乙的平均分为
,乙的平均分为![]() ,
,
甲的分数=![]() =90.4,
=90.4,
乙的分数=![]() =90.95.
=90.95.
(4)选乙,理由:90.95>90.4,乙的分数高.
故选乙.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】最早对勾股定理进行证明的,是三国时期吴国的数学家赵爽,赵爽创制了一幅“勾股圆方图”,用数形结合的方法,给出了勾股定理的详细证明.在这幅“勾股圆方图”中,以弦为边长得到的正方形是由4个全等的直角三角形再加上中间的小正方形组成的.设直角三角形的两直角边长为![]() ,且满足
,且满足![]() ,若小正方形的面积为11,则大正方形的面积为( )
,若小正方形的面积为11,则大正方形的面积为( )

A.15B.17C.30D.34
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数的图象与x轴相交于A(3,0)、B(1,0)两点,与y轴相交于点C(0,3),点C.D是二次函数图象上的一对对称点,一次函数的图象过点B,D.
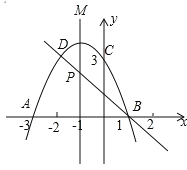
(1)D点坐标;
(2)求二次函数的解析式;
(3)根据图象直接写出使一次函数值小于二次函数值的x的取值范围;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,∠B=90°,AD∥BC,且AD=4cm,AB=6cm,DC=10cm.若动点P从A点出发,以每秒4cm的速度沿线段AD、DC向C点运动;动点Q从C点出发以每秒5cm的速度沿CB向B点运动,当Q点到达B点时,动点P、Q同时停止运动.设点P、Q同时出发,并运动了t秒.
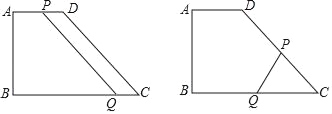
(1)当t为多少秒时,四边形PQCD是平行四边形?请说明理由;
(2)当t为多少秒时,AQ=DC?请说明理由;
(3)当t为多少秒时,PQ⊥DC?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】电器专营店的经营利润受地理位置、顾客消费能力等因素的影响,某品牌电脑专营店设有甲、乙两家分店,均销售A、B、C、D四种款式的电脑,每种款式电脑的利润如表1所示.现从甲、乙两店每月售出的电脑中各随机抽取所记录的50台电脑的款式,统计各种款式电脑的销售数量,如表2所示.
表1:四种款式电脑的利润
电脑款式 | A | B | C | D |
利润(元/台) | 160 | 200 | 240 | 320 |
表2:甲、乙两店电脑销售情况
电脑款式 | A | B | C | D |
甲店销售数量(台) | 20 | 15 | 10 | 5 |
乙店销售数量(台)8 | 8 | 10 | 14 | 18 |
试运用统计与概率知识,解决下列问题:
(1)从甲店每月售出的电脑中随机抽取一台,其利润不少于240元的概率为 ;
(2)经市场调查发现,甲、乙两店每月电脑的总销量相当.现由于资金限制,需对其中一家分店作出暂停营业的决定,若从每台电脑的平均利润的角度考虑,你认为应对哪家分店作出暂停营业的决定?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
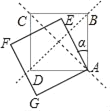
【题目】如图,当α=0°时,正方形ABCD与正方形AEFG互相重合,现将正方形AEFG绕点A逆时针旋转,当α=_____时(0°<α<360°),正方形AEFG的顶点F会落在正方形ABCD的两对角线AC或BD所在直线上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,△ABC中,∠ACB=90°,AC=4,BC=6,点E,F分别在边AB,BC上,将△ABC沿直线EF折叠,点B恰好落在AC边上的点D处,且CD=3.
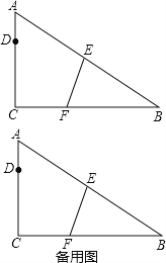
(1)求CF的长;
(2)点G是射线BA上的一个动点,连接DG,GC,BD,△DGC的面积与△DGB的面积相等,
①当点G在线段BA上时,求BG的长;
②当点G在线段BA的延长线上时,BG=______;
(3)将直线EF平移,平移后的直线与直线BC,直线AC分别交于点M和点N,以线段MN为一边作正方形MNPQ,点P与点B在直线MN两侧,连接PD,当PD∥BC时,请直接写出tan∠QBC的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com