
 13、如图,在实践活动课上,小明同学用纸板制作了一个圆锥形漏斗模型.如图所示,它的底面半径OB=3cm,高OC=4cm,则这个圆锥漏斗的侧面积是
13、如图,在实践活动课上,小明同学用纸板制作了一个圆锥形漏斗模型.如图所示,它的底面半径OB=3cm,高OC=4cm,则这个圆锥漏斗的侧面积是
 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
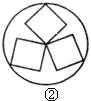
 8、在综合实践活动课上,小红准备用两种不同颜色的布料缝制一个正方形座垫,座垫的图案如图所示,应该选下图中的哪一块布料才能使其与右图拼接符合原来的图案模式( )
8、在综合实践活动课上,小红准备用两种不同颜色的布料缝制一个正方形座垫,座垫的图案如图所示,应该选下图中的哪一块布料才能使其与右图拼接符合原来的图案模式( )查看答案和解析>>
科目:初中数学 来源: 题型:
 校园内有一个高大的树,在实践活动课上,准备了如下测量工具“皮尺”、“高为1米的测角器”、“长为2米的标杆”来测量树的高度,请你设计测量方案并回答下列问题.
校园内有一个高大的树,在实践活动课上,准备了如下测量工具“皮尺”、“高为1米的测角器”、“长为2米的标杆”来测量树的高度,请你设计测量方案并回答下列问题.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 校园内有一个高大的树,在实践活动课上,准备了如下测量工具“皮尺”、“高为1米的测角器”、“长为2米的标杆”来测量树的高度,请你设计测量方案并回答下列问题.
校园内有一个高大的树,在实践活动课上,准备了如下测量工具“皮尺”、“高为1米的测角器”、“长为2米的标杆”来测量树的高度,请你设计测量方案并回答下列问题.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com