
【题目】在平面直角坐标系中,已知:函数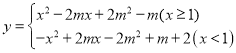 .
.
(1)当![]() 时,
时,
①求![]() 随
随![]() 增大而增大时,
增大而增大时,![]() 的取值范围;
的取值范围;
②当![]() 时,求
时,求![]() 的取值范围;
的取值范围;
③当![]() 时,设
时,设![]() 的最大值与最小值之差为
的最大值与最小值之差为![]() ,当
,当![]() 时,求
时,求![]() 的值.
的值.
(2)若![]() ,连结
,连结![]() .当此函数的图象与线段
.当此函数的图象与线段![]() 只有两个公共点时,直接写出
只有两个公共点时,直接写出![]() 的取值范围.
的取值范围.
【答案】(1)①![]() 或
或![]() ;②
;②![]() ;③
;③![]() 或
或![]() ;(2)
;(2)![]() 或
或![]() 或
或![]() .
.
【解析】
(1)①利用函数图像,直接作答即可;
②观察函数图像直接作答即可;
③分![]() 、
、![]() 、
、![]() 、
、![]() 四种情况分类讨论即可;
四种情况分类讨论即可;
(2)利用两个函数的对称轴都是直线![]() ,分类讨论
,分类讨论![]() 所处的位置,即可得出答案.
所处的位置,即可得出答案.
(1)①![]() 或
或![]() .
.
当![]() 时,函数变为
时,函数变为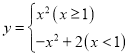 ,
,
函数图像如图所示:
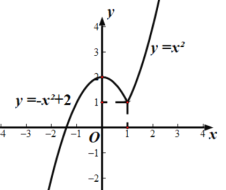
函数![]() 的对称轴是直线
的对称轴是直线![]() ,
,
所以通过观察图像可以得到当![]() 随
随![]() 增大而增大时,
增大而增大时,![]() 的取值范围是:
的取值范围是:![]() 或
或![]() ;
;
②![]() ;
;
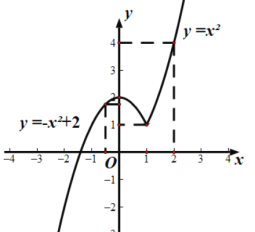
通过观察图像可以得到:当![]() 时,
时,![]() ;
;
③当![]() ,即
,即![]() 时,
时,
![]()
![]() ,
,![]()
当![]() 时,由图象可知
时,由图象可知![]()
当![]() 时,
时,![]()
由![]() ,
,
得![]() ,
,
![]()
![]()
当![]() 时,
时,![]()
![]()
![]()
![]() 舍去.
舍去.
综上所述:![]() 或
或![]() ;
;

![]() 或
或![]() 或
或![]() ,
,
∵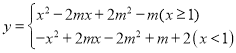
∴![]() 的对称轴为直线:
的对称轴为直线:![]() ,
,
![]() 的对称轴为直线:
的对称轴为直线:![]() ,
,
①由(1)可知:当![]() 时,函数与AB有两个交点,一个为(0,2),一个为(
时,函数与AB有两个交点,一个为(0,2),一个为(![]() ),满足条件;
),满足条件;
②当![]() 时,函数变为:
时,函数变为: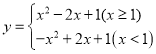 ,此时只有一个交点
,此时只有一个交点![]() ,不合题意;
,不合题意;
③当![]() 时,函数变为:
时,函数变为: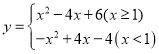 ,此时只有一个交点
,此时只有一个交点![]() ,不合题意;
,不合题意;
④当![]() 时,此时
时,此时![]() 的顶点坐标为
的顶点坐标为![]() ,
,
∵![]() ,
,
∴![]() 与AB无交点;
与AB无交点;
对于函数![]() 一直小于0,因此与AB无交点;
一直小于0,因此与AB无交点;
⑤当![]() 时,
时,
对于函数![]() 来说,当
来说,当![]() 时,有最小值此时
时,有最小值此时![]() ,因此函数
,因此函数![]() 与AB最多有一个交点,
与AB最多有一个交点,
对于函数![]() ,当
,当![]() 时,有最大值,为
时,有最大值,为![]() ,与AB无交点;
,与AB无交点;
⑥当![]() 时,
时,
对于函数![]() 来说,
来说,![]() ,因此与AB必有一个交点,
,因此与AB必有一个交点,
只须保证:![]() 与AB有一个交点即可,
与AB有一个交点即可,
当![]() 时,当
时,当![]() 时,有最大值为
时,有最大值为![]() ,根据对称性可知:此时与AB有两个交点,
,根据对称性可知:此时与AB有两个交点,
∴当![]() 时,有三个交点,不合题意;
时,有三个交点,不合题意;
当![]() 时,
时,
函数变为: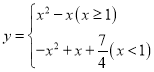 ,此时与AB共有两个交点;
,此时与AB共有两个交点;
当![]() 时:
时:![]() 与AB有一个交点,
与AB有一个交点,
∴此时函数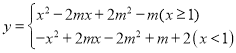 与AB有两个交点;
与AB有两个交点;
⑦当![]() 时,
时,
对于函数![]() :
:![]() ,与AB无交点,
,与AB无交点,
当函数![]() 过
过![]() 时,
时,
得:![]() ,解得:
,解得:![]() ,
,
∵![]() ,
,
∴![]() ,此时与AB有两个交点,
,此时与AB有两个交点,
∴当![]() 时,
时,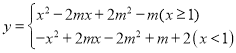 与AB有两个交点;
与AB有两个交点;
综上所述:当![]() 或
或![]() 或
或![]() 时,
时,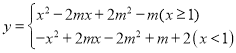 与AB只有两个交点.
与AB只有两个交点.


 新思维寒假作业系列答案
新思维寒假作业系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知点A,对点A作如下变换:
第一步:作点A关于x轴的对称点A1;第二步:以O为位似中心,作线段OA1的位似图形OA2,且相似比![]() =q,则称A2是点A的对称位似点.
=q,则称A2是点A的对称位似点.
(1)若A(2,3),q=2,直接写出点A的对称位似点的坐标;
(2)已知直线l:y=kx-2,抛物线C:y=-![]() x2+mx-2(m>0).点N(
x2+mx-2(m>0).点N(![]() ,2k-2)在直线l上.
,2k-2)在直线l上.
①当k=![]() 时,判断E(1,-1)是否是点N的对称位似点,请说明理由;
时,判断E(1,-1)是否是点N的对称位似点,请说明理由;
②若直线l与抛物线C交于点M(x1,y1)(x1≠0),且点M不是抛物线的顶点,则点M的对称位似点是否可能仍在抛物线C上?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司销售的一种时令商品每件成本为20元,经过市场调查分析,5月份的日销售件数为:![]() (其中t为天数),并且前15天,每天的价格
(其中t为天数),并且前15天,每天的价格![]() (元/件)与时间t(天)的函数关系式为
(元/件)与时间t(天)的函数关系式为![]() (
(![]() ,且t为整数),第16天到月底每天的价格
,且t为整数),第16天到月底每天的价格![]() (元/件)与时间t(天)的函数关系式为
(元/件)与时间t(天)的函数关系式为![]() (
(![]() ,且t为整数),根据以上信息,解答下列问题:
,且t为整数),根据以上信息,解答下列问题:
(1)5月份第10天的销售件数为________件,销售利润为________元;
(2)请通过计算预测5月份中哪一天的日销售利润w最大,最大日销售利润是多少?
(3)在实际销售的前15天中,该公司决定每销售一件商品就捐赠m元利润![]() 给希望工程.公司通过销售记录发现,前15天中,每天扣除捐赠后的日销售利润w随t的增大而增大,求m的取值范围.
给希望工程.公司通过销售记录发现,前15天中,每天扣除捐赠后的日销售利润w随t的增大而增大,求m的取值范围.
参考公式:抛物线![]() 的顶点坐标是
的顶点坐标是 .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在每个边长都为![]() 的小正方形组成的网格中,小正方形的顶点叫做格点.线段
的小正方形组成的网格中,小正方形的顶点叫做格点.线段![]() 的端点
的端点![]() 均在格点上.
均在格点上.
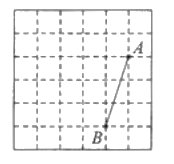
(1)线段![]() 的长度等于 ;
的长度等于 ;
(2)将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,在图中画出
,在图中画出![]() ,并连结
,并连结![]() .
.
(3)在线段![]() 上确定一点
上确定一点![]() 连结
连结![]() ,使得
,使得![]() 与
与![]() 的面积比为
的面积比为![]() .
.
说明:以上作图只用无刻度的直尺画图,保留画图痕迹,不写画法.
查看答案和解析>>
科目:初中数学 来源: 题型:
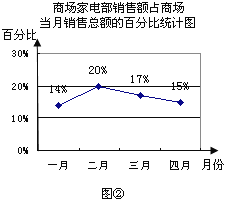
【题目】图①表示的是某商场2012年前四个月中两个月的商品销售额的情况,图②表示的是商场家电部各月销售额占商场当月销售总额的百分比情况,观察图①、图②解答下列问题:
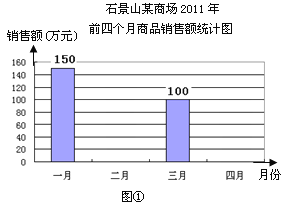
(1)商场前四个月财务结算显示四月份商场的商品销售额比一月份下降了20%,请你求出商场四月份的销售额;
(2)若商场前四个月的商品销售总额一共是500万元,请你根据这一信息将图①中的统计图补充完整;
(3)小明观察图②后认为,商场家电部四月份的销售额比三月份减少了,你同意他的看法吗?请你说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某玩具店进了一排黑白塑料球,共5箱,每箱的规格、数量都相同,其中每箱中装有黑白两种颜色的塑料球共3000个,为了估计每箱中两种颜色球的个数,随机抽查了一箱,将箱子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回箱子中,多次重复上述过程后,发现摸到黑球的概率在0.8附近波动,则此可以估计这批塑料球中黑球的总个数,请将黑球总个数用科学记数法表示约为________个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,张老师举了下面的例题:
例1 等腰三角形![]() 中,
中,![]() ,求
,求![]() 的度数.(答案:
的度数.(答案:![]() )
)
例2 等腰三角形![]() 中,
中,![]() ,求
,求![]() 的度数.(答案:
的度数.(答案:![]() 或
或![]() 或
或![]() )
)
张老师启发同学们进行变式,小敏编了如下一题:
变式 等腰三角形![]() 中,
中,![]() ,求
,求![]() 的度数.
的度数.
(1)请你解答以上的变式题.
(2)解(1)后,小敏发现,![]() 的度数不同,得到
的度数不同,得到![]() 的度数的个数也可能不同.如果在等腰三角形
的度数的个数也可能不同.如果在等腰三角形![]() 中,设
中,设![]() ,当
,当![]() 有三个不同的度数时,请你探索
有三个不同的度数时,请你探索![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
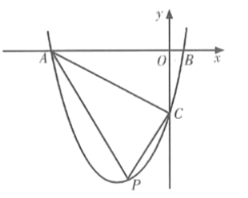
【题目】如图,在平面直角坐标系中,抛物线![]() 交
交![]() 轴于
轴于![]() ,
,![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,且
,且![]() ,点
,点![]() 是第三象限内抛物线上的一动点.
是第三象限内抛物线上的一动点.
(1)求此抛物线的表达式;
(2)若![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)连接![]() ,求
,求![]() 面积的最大值及此时点
面积的最大值及此时点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com