
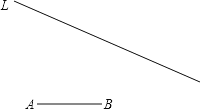
【题目】在数学课上,爱动脑筋的小孙同学提出了一个问题:已知线段AB和直线L,他想作一个顶点P在直线上L的特殊的![]() ,使得
,使得![]()
经过课堂讨论,有的学习小组提出了如下尺规作图方案:
![]() 分别以点A,点B为圆心,以线段AB的长度为半径画弧,两条弧在线段AB上方相交于点O;
分别以点A,点B为圆心,以线段AB的长度为半径画弧,两条弧在线段AB上方相交于点O;
![]() 以O为圆心,OA为半径作弧,与直线L相交于
以O为圆心,OA为半径作弧,与直线L相交于![]() ,
,![]() 两点;
两点;
![]() 连接
连接![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() 就是所求的角
就是所求的角
请你根据上述尺规作图方案,完成下列问题:
![]() 使用直尺和圆规补全图形;
使用直尺和圆规补全图形;![]() 保留作图痕迹
保留作图痕迹![]()
![]() 完成下面的证明:
完成下面的证明:
证明:在![]() 中,连接OA,OB,
中,连接OA,OB,
![]() 为等边三角形
为等边三角形![]() ______
______![]() 填推理的依据
填推理的依据![]()
![]() ,
,![]()
![]() ______
______![]() 填推理的依据
填推理的依据![]()
科目:初中数学 来源: 题型:
【题目】如图,以40m/s的速度将小球沿与地面成30°角的方向击出时,小球的飞行路线是一条抛物线.如果不考虑空气阻力,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有函数关系h=20t﹣5t2.
(1)小球飞行时间是多少时,小球最高?最大高度是多少?
(2)小球飞行时间t在什么范围时,飞行高度不低于15m?
查看答案和解析>>
科目:初中数学 来源: 题型:
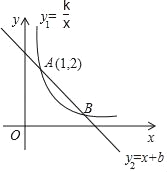
【题目】反比例函数y1=![]() (x>0)的图象与一次函数y2=﹣x+b的图象交于A,B两点,其中A(1,2)
(x>0)的图象与一次函数y2=﹣x+b的图象交于A,B两点,其中A(1,2)
(1)求这两个函数解析式;
(2)在y轴上求作一点P,使PA+PB的值最小,并直接写出此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,下面说法正确的个数是( )个.
①若O是△ABC的外心,∠A=50°,则∠BOC=100°;
②若O是△ABC的内心,∠A=50°,则∠BOC=115°;
③若BC=6,AB+AC=10,则△ABC的面积的最大值是12;
④△ABC的面积是12,周长是16,则其内切圆的半径是1.

A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列判断正确的是![]()
![]()
A. “打开电视机,正在播NBA篮球赛”是必然事件
B. “掷一枚硬币正面朝上的概率是![]() ”表示毎抛掷硬币2次就必有1次反面朝上
”表示毎抛掷硬币2次就必有1次反面朝上
C. 一组数据2,3,4,5,5,6的众数和中位数都是5
D. 甲组数据的方差![]() ,乙组数据的方差
,乙组数据的方差![]() ,则乙组数据比甲组数据稳定
,则乙组数据比甲组数据稳定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠BAC=90°,过点B的直线MN∥AC,D为BC边上一点,连接AD,作DE⊥AD交MN于点E,连接AE.
(1)如图①,当∠ABC=45°时,求证:AD=DE;理由;
(2)如图②,当∠ABC=30°时,线段AD与DE有何数量关系?并请说明理由;
(3)当∠ABC=α时,请直接写出线段AD与DE的数量关系.(用含α的三角函数表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
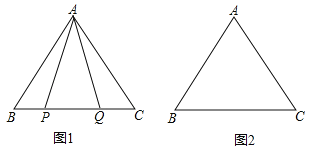
【题目】在等边△ABC中:
(1)如图1,P,Q是BC边上的两点,AP=AQ,∠BAP=20°,求∠AQB的度数;
(2)点P,Q是BC边上的两个动点(不与点B,C重合),点P在点Q的左侧,且AP=AQ,点Q关于直线AC的对称点为M,连接AM,PM.
①依题意将图2补全;
②小茹通过观察、实验提出猜想:在点P,Q运动的过程中,始终有PA=PM,小茹把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:要证明PA=PM,只需证△APM是等边三角形;
想法2:在BA上取一点N,使得BN=BP,要证明PA=PM,只需证△ANP≌△PCM;
想法3:将线段BP绕点B顺时针旋转60°,得到线段BK,要证PA=PM,只需证PA=CK,PM=CK…
请你参考上面的想法,帮助小茹证明PA=PM(一种方法即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
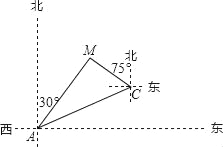
【题目】如图,某天然气公司的主输气管道从A市的北偏东60°方向直线延伸,测绘员在A处测得要安装天然气的M小区在A市的北偏东30°方向,测绘员沿主输气管道步行1000米到达C处,测得小区M位于点C的北偏西75°方向,试在主输气管道AC上寻找支管道连接点N,使其到该小区铺设的管道最短,并求AN的长.(精确到1米,![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=﹣x2+bx+c(c>0)的图象与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,且OB=OC=3,顶点为M.
(1)求二次函数的解析式;
(2)点P为线段BM上的一个动点,过点P作x轴的垂线PQ,垂足为Q,若OQ=m,四边形ACPQ的面积为S,求S关于m的函数解析式,并写出m的取值范围;
(3)探索:线段BM上是否存在点N,使△NMC为等腰三角形?如果存在,求出点N的坐标;如果不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com