解:(1)抛物线y=ax
2+bx+3经过A(-3,0),B(-1,0)两点:
∴
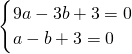
解得:a=1,b=4,
(2)由 (1)求得抛物线的解析式为y=x
2+4x+3,
配方得y=(x+2)
2-1
∴抛物线的顶点M(-2,-1),
∴直线OD的解析式为y=

x,
由方程组
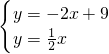
,解得:
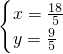
,
∴D(

,

)
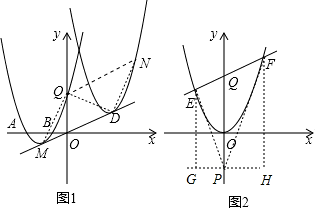
如图1,由平移的性质知,抛物线上的两点M、Q间所夹的曲线
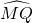
扫过的区域的面积即为平行四边形MDNQ的面积,连接QD,
∴S
平行四边形MDNQ=2S
△MDQ=2(S
△OQM+S
△OQD)=
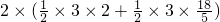
=
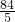
;
(3)由(2)知抛物线的顶点M(-2,-1),直线OD的解析式为y=

x,于是设平移的抛物线的顶点坐标为(h,

h),
∴平移的抛物线解析式为y=(x-h)
2+

h.
①当抛物线经过点C时,
∵C(0,9),
∴h
2+

h=9,解得
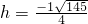
.
∴当
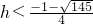
时,平移的抛物线与射线CD没有公共点.
②当抛物线与直线CD没有公共点时,由方程组
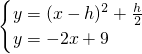
,
消去y得:
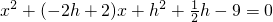
,
∴△=
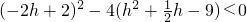
,
∴h>4.
此时抛物线y=(x-4)
2+2与直线CD没有公共点.从而与射线CD没有共公点.
综上由①、②可知:平移后的抛物线与射线CD没有公共点时,顶点横坐标的取值范围是:
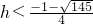
或h>4
(4)将抛物线平移,当顶点至原点时,其解析式为y=x
2,
设EF的解析式为y=k x+3(k≠0).假设存在满足题设条件的点P(0,t)过P作GH∥x轴,分别过E,F作GH的垂线,
垂足为G,H(如图2).
∵∠EPQ=∠QPF,
∴∠GEP=∠EPQ=∠QPF=∠HFP,
∴△GEP∽△HFP,
∴
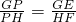
,
∴
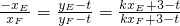
∴2k x
E•x
F=(t-3)(x
E+x
F)
由
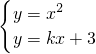
. 得x
2-kx-3=0.
∴x
E+x
F=k,x
E•x
F=-3.
∴2k(-3)=(t-3)k
∵k≠0,
∴t=-3.
∴y轴的负半轴上存在点P(0,-3),使∠EPQ=∠QPF.
分析:(1)将已知的两点的坐标代入二次函数的解析式利用待定系数法求得a、b的值即可;
(2)首先将求得的抛物线的解析式利用配方法求得其顶点坐标,然后求得D点的坐标,3然后利用平移的性质即可求得平行四边形MDNQ的面积;
(3)由(2)知抛物线的顶点M(-2,1),直线OD的解析式为y=

x,于是设平移的抛物线的顶点坐标为(h,

h),从而确定平移的抛物线解析式为y=(x-h)
2+

h.然后分当抛物线经过点C和当抛物线与直线CD没有公共点两种情况求得h的值或取值范围即可;
(4)将抛物线平移,当顶点至原点时,其解析式为y=x
2,设EF的解析式为y=k x+3(k≠0).假设存在满足题设条件的点P(0,t)过P作GH∥x轴,分别过E,F作GH的垂线通过证明△GEP∽△HFP得到比例式求得t值即可存在,否则就不存在.
点评:本题主要考查了二次函数解析式的确定、函数图象交点的求法等知识点.主要考查学生数形结合的数学思想方法.

 扫过的区域的面积;
扫过的区域的面积;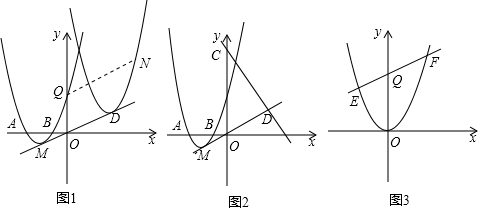
 解:(1)抛物线y=ax2+bx+3经过A(-3,0),B(-1,0)两点:
解:(1)抛物线y=ax2+bx+3经过A(-3,0),B(-1,0)两点: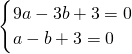 解得:a=1,b=4,
解得:a=1,b=4, x,
x,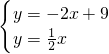 ,解得:
,解得: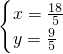 ,
, ,
, )
)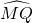 扫过的区域的面积即为平行四边形MDNQ的面积,连接QD,
扫过的区域的面积即为平行四边形MDNQ的面积,连接QD,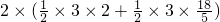 =
=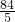 ;
; x,于是设平移的抛物线的顶点坐标为(h,
x,于是设平移的抛物线的顶点坐标为(h, h),
h), h.
h. h=9,解得
h=9,解得 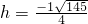 .
.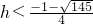 时,平移的抛物线与射线CD没有公共点.
时,平移的抛物线与射线CD没有公共点.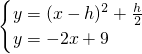 ,
,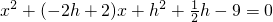 ,
,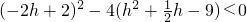 ,
,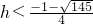 或h>4
或h>4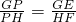 ,
,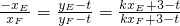
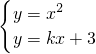 . 得x2-kx-3=0.
. 得x2-kx-3=0. x,于是设平移的抛物线的顶点坐标为(h,
x,于是设平移的抛物线的顶点坐标为(h, h),从而确定平移的抛物线解析式为y=(x-h)2+
h),从而确定平移的抛物线解析式为y=(x-h)2+ h.然后分当抛物线经过点C和当抛物线与直线CD没有公共点两种情况求得h的值或取值范围即可;
h.然后分当抛物线经过点C和当抛物线与直线CD没有公共点两种情况求得h的值或取值范围即可;

 与x轴的另一个交点为E.
与x轴的另一个交点为E. 如图,已知抛物线y=ax2+bx+c(其中b>0,c<0)的顶点P在x轴上,与y轴交于点Q,过坐标原点O,作OA⊥PQ,垂足为A,且OA=
如图,已知抛物线y=ax2+bx+c(其中b>0,c<0)的顶点P在x轴上,与y轴交于点Q,过坐标原点O,作OA⊥PQ,垂足为A,且OA=