
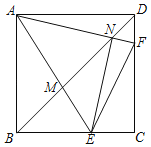
【题目】如图,在正方形ABCD中,E、F分别是BC、CD上的点,且∠EAF=45°,AE、AF分别交BD于M、N,连按EN、EF、有以下结论:①AN=EN,②当AE=AF时,![]() =2﹣
=2﹣![]() ,③BE+DF=EF,④存在点E、F,使得NF>DF,其中正确的个数是( )
,③BE+DF=EF,④存在点E、F,使得NF>DF,其中正确的个数是( )
A. 1B. 2C. 3D. 4
【答案】B
【解析】
①如图1,证明△AMN∽△BME和△AMB∽△NME,可得∠NAE=∠AEN=45°,则△AEN是等腰直角三角形可作判断;
②先证明CE=CF,假设正方形边长为1,设CE=x,则BE=1-x,表示AC的长为AO+OC可作判断;
③如图3,将△ADF绕点A顺时针旋转90°得到△ABH,证明△AEF≌△AEH(SAS),则EF=EH=BE+BH=BE+DF,可作判断;
④在△ADN中根据比较对角的大小来比较边的大小.
①如图1,
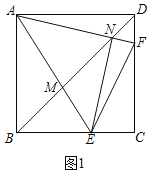
∵四边形ABCD是正方形,
∴∠EBM=∠ADM=∠FDN=∠ABD=45°,
∵∠MAN=∠EBM=45°,∠AMN=∠BME,
∴△AMN∽△BME,
∴![]() ,
,
∵∠AMB=∠EMN,
∴△AMB∽△NME,
∴∠AEN=∠ABD=45°
∴∠NAE=∠AEN=45°,
∴△AEN是等腰直角三角形,
∴AN=EN,
故①正确;
②在△ABE和△ADF中,
∵ ,
,
∴Rt△ABE≌Rt△ADF(HL),
∴BE=DF,
∵BC=CD,
∴CE=CF,
假设正方形边长为1,设CE=x,则BE=1﹣x,
如图2,连接AC,交EF于H,

∵AE=AF,CE=CF,
∴AC是EF的垂直平分线,
∴AC⊥EF,OE=OF,
Rt△CEF中,OC=![]() EF=
EF=![]() x,
x,
△EAF中,∠EAO=∠FAO=22.5°=∠BAE=22.5°,
∴OE=BE,
∵AE=AE,
∴Rt△ABE≌Rt△AOE(HL),
∴AO=AB=1,
∴AC=![]() =AO+OC,
=AO+OC,
∴1+![]() x=
x=![]() ,
,
x=2﹣![]() ,
,
∴![]() =
=![]() =
=![]() =
=![]() ;
;
故②不正确;
③如图3,

∴将△ADF绕点A顺时针旋转90°得到△ABH,则AF=AH,∠DAF=∠BAH,
∵∠EAF=45°=∠DAF+∠BAE=∠HAE,
∵∠ABE=∠ABH=90°,
∴H、B、E三点共线,
在△AEF和△AEH中,
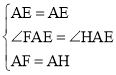 ,
,
∴△AEF≌△AEH(SAS),
∴EF=EH=BE+BH=BE+DF,
故③正确;
④△ADN中,∠FND=∠ADN+∠NAD>45°,
∠FDN=45°,
∴DF>FN,
故存在点E、F,使得NF>DF,
故④不正确;
故选B.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A出发沿AB以1cm/s的速度向点B移动;同时,点Q从点B出发沿BC以2cm/s的速度向点C移动.设运动时间为t秒.
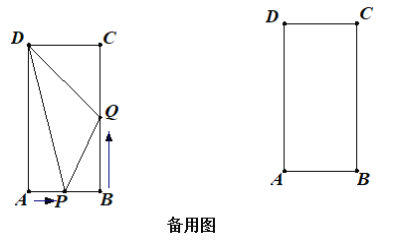
(1)当t=2时,△DPQ的面积为 cm2;
(2)在运动过程中△DPQ的面积能否为26cm2?如果能,求出t的值,若不能,请说明理由;
(3)运动过程中,当 A、P、Q、D四点恰好在同一个圆上时,求t的值;
(4)运动过程中,当以Q为圆心,QP为半径的圆,与矩形ABCD的边共有4个交点时,直接写出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=a(x﹣h)2+k(a≠0)的图象是抛物线,定义一种变换,先作这条抛物线关于原点对称的抛物线y′,再将得到的对称抛物线y′向上平移m(m>0)个单位,得到新的抛物线ym,我们称ym叫做二次函数y=a(x﹣h)2+k(a≠0)的m阶变换.
(1)已知:二次函数y=2(x+2)2+1,它的顶点关于原点的对称点为 ,这个抛物线的2阶变换的表达式为 .
(2)若二次函数M的6阶变换的关系式为y6′=(x﹣1)2+5.
①二次函数M的函数表达式为 .
②若二次函数M的顶点为点A,与x轴相交的两个交点中左侧交点为点B,在抛物线y6′=(x﹣1)2+5上是否存在点P,使点P与直线AB的距离最短,若存在,求出此时点P的坐标.
(3)抛物线y=﹣3x2﹣6x+1的顶点为点A,与y轴交于点B,该抛物线的m阶变换的顶点为点C.若△ABC是以AB为腰的等腰三角形,请直按写出m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子中装有4张卡片.4张卡片的正面分别标有数字1,2,3,4,这些卡片除数字外都相同,将卡片搅匀.
(1)从盒子任意抽取一张卡片,恰好抽到标有奇数卡片的概率是: ;
(2)先从盒子中任意抽取一张卡片,再从余下的3张卡片中任意抽取一张卡片,求抽取的2张卡片标有数字之和大于4的概率(请用画树状图或列表等方法求解).
查看答案和解析>>
科目:初中数学 来源: 题型:
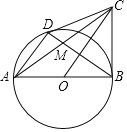
【题目】如图,已知AB是⊙O的直径,CB⊥AB,D为圆上一点,且AD∥OC,连接CD,AC,BD,AC与BD交于点M.
(1)求证:CD为⊙O的切线;
(2)若CD=![]() AD,求
AD,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
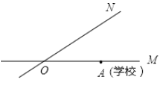
【题目】如图,有两条公路OM,ON相交成30°,沿公路OM方向离两条公路的交叉处O点80米的A处有一所希望小学,当拖拉机沿ON方向行驶时,距拖拉机中心50米的范围内均会受到噪音影响,已知有两台相距40米的拖拉机正沿ON方向行驶,它们的速度均为10米/秒,则这两台拖拉机沿ON方向行驶时给小学带来噪音影响的时间为 ( )
A. 6秒B. 8秒C. 10秒D. 18秒
查看答案和解析>>
科目:初中数学 来源: 题型:
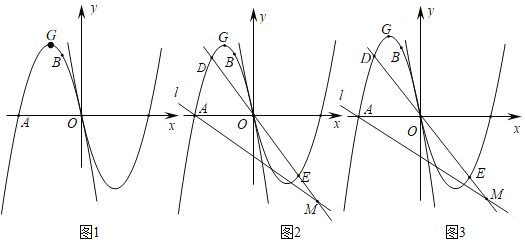
【题目】如图1,抛物线![]() 经过点
经过点![]() 、
、![]() 两点,
两点,![]() 是其顶点,将抛物线
是其顶点,将抛物线![]() 绕点
绕点![]() 旋转
旋转![]() ,得到新的抛物线
,得到新的抛物线![]() .
.
(1)求抛物线![]() 的函数解析式及顶点
的函数解析式及顶点![]() 的坐标;
的坐标;
(2)如图2,直线![]() 经过点
经过点![]() ,
,![]() 是抛物线
是抛物线![]() 上的一点,设
上的一点,设![]() 点的横坐标为
点的横坐标为![]() (
(![]() ),连接
),连接![]() 并延长,交抛物线
并延长,交抛物线![]() 于点
于点![]() ,交直线l于点
,交直线l于点![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)如图3,在(2)的条件下,连接![]() 、
、![]() ,在直线
,在直线![]() 下方的抛物线
下方的抛物线![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ?若存在,求出点
?若存在,求出点![]() 的横坐标;若不存在,请说明理由.
的横坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com