把直线y=-x+3向上平移m个单位后,与直线y=2x+4的交点在第一象限,则m的取值范围是( )
A.1<m<7
B.3<m<4
C.m>1
D.m<4
【答案】
分析:直线y=-x+3向上平移m个单位后可得:y=-x+3+m,求出直线y=-x+3+m与直线y=2x+4的交点,再由此点在第一象限可得出m的取值范围.
解答:解:直线y=-x+3向上平移m个单位后可得:y=-x+3+m,
联立两直线解析式得:

,
解得:

,
即交点坐标为(
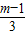
,
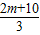
),
∵交点在第一象限,
∴

,
解得:m>1.
故选C.
点评:本题考查了一次函数图象与几何变换、两直线的交点坐标,注意第一象限的点的横、纵坐标均大于0.
