
 如图,有一块四边形形状的铁皮ABCD,BC=CD=6,AB=2AD,∠ABC=∠ADB=90°,以C为圆心,CB为半径作弧BD得一扇形CBD,剪下扇形并用它围成一圆锥的侧面.
如图,有一块四边形形状的铁皮ABCD,BC=CD=6,AB=2AD,∠ABC=∠ADB=90°,以C为圆心,CB为半径作弧BD得一扇形CBD,剪下扇形并用它围成一圆锥的侧面.分析 (1)由已知条件可得∠DBC=30°,所以∠DBC=60°,则△CDB为等边三角形,进而求出∠C的度数;
(2)利用弧长公式可以求出弧BD的长,即圆锥底面圆的周长,从而求出圆的半径.
解答 解:(1)∵∠ABC=90°,AB=2AD,
∴sin∠ABD=$\frac{AD}{AB}$=$\frac{1}{2}$,
∴∠ABD=30°,
∵∠ADB=90°,
∴∠DBC=90°-30°=60°,
∵BC=CD=6,
∴△CBD是等边三角形,
∴∠BCD=60°;
(2)∵${l}_{\widehat{BD}}$=$\frac{60π×12}{180}$=2π,
∴2π=2πr,
∴r=1.
点评 本题考查了直角三角形的性质、等边三角形的判定和等边三角形的性质以及考查有关扇形和圆锥的相关计算.解题思路:解决此类问题时要紧紧抓住两者之间的两个对应关系:(1)圆锥的母线长等于侧面展开图的扇形半径;(2)圆锥的底面周长等于侧面展开图的扇形弧长.正确对这两个关系的记忆是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
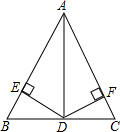 如图,在△ABC中,AD平分∠BAC,且BD=CD,DE⊥AB于点E,DF⊥AC于点F.
如图,在△ABC中,AD平分∠BAC,且BD=CD,DE⊥AB于点E,DF⊥AC于点F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3.0037×1013元 | B. | 3.00×1013元 | C. | 30.1×1012元 | D. | 3.01×1013元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com