练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

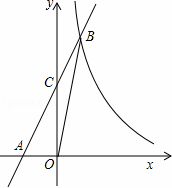
    如图，在平面直角坐标系xOy中，一次函数y=ax+b的图象与x轴相交于点A（﹣2，0），与y轴交于点C，与反比例函数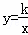在第一象限内的图象交于点B（m，n），连结OB．若S△AOB=6，S△BOC=2．

    （1）求一次函数的表达式；

    （2）求反比例函数的表达式．


    解：（1）∵S△AOB=6，S△BOC=2，

    ∴S△AOC=4，

    ∴•2•OC=4，解得OC=4，

    ∴C点坐标为（0，4），

    设一次函数解析式为y=mx+n，

    把A（﹣2，0），C（0，4）代入得，解得，

    ∴一次函数解析式为y=2x+4；

    （2）∵S△BOC=2，

    ∴×4×m=2，解得m=1，

    ∴B点坐标为（1，6），

    把B（1，6）代入y=得k=1×6=6，

    ∴反比例函数解析式为y=．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


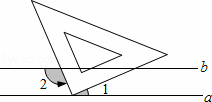
    如图，已知a∥b，小华把三角板的直角顶点放在直线b上．若∠1=40°，则∠2的度数为（　　）

    　

    A．

    100°

    B．

    110°

    C．

    120°

    D．

    130°

    查看答案和解析>>

    科目：初中数学 来源： 题型：


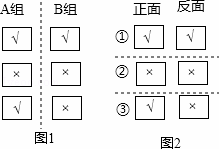
    有六张完全相同的卡片，分A，B两组，每组三张，在A组的卡片上分别画上“√，×，×”，如图1．

    （1）若将卡片无标记的一面朝上摆在桌上再分别从两组卡片中随机各抽取一张，求两张卡片上标记都是“√”的概率．（请用“树形图法”或“列表法“求解）

    （2）若把A，B两组卡片无标记的一面对应粘贴在一起得到三张卡片，其正、反面标记如图2所示，将卡片正面朝上摆在桌上，并用瓶盖盖住标记．

    ①若随机揭开其中一个盖子，看到的标记是“√”的概率是多少？

    ②若揭开盖子，看到的卡片正面标记是“√”后，猜想它的反面也是“√”，求猜对的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    若，则xy﹣3的值为　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    有一列数如下：1，0，1，0，0，1，0，0，0，1，0，0，0，0，1，…，则第9个1在这列数中是第　 　个数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


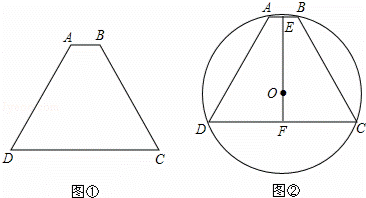
    如图①，已知等腰梯形ABCD的周长为48，面积为S，AB∥CD，∠ADC=60°，设AB=3x．

    （1）用x表示AD和CD；

    （2）用x表示S，并求S的最大值；

    （3）如图②，当S取最大值时，等腰梯形ABCD的四个顶点都在⊙O上，点E和点F分别是AB和CD的中点，求⊙O的半径R的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    甲口袋中有1个红球和1个黄球，乙口袋中有1个红球、1个黄球和1个绿球，这些球除颜色外都相同．从两个口袋中各随机取一个球，取出的两个球都是红的概率为（　　）

    　

    A．

    B．

    C．

    D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，矩形纸片ABCD中，AB=6，BC=8．折叠纸片使点B落在AD上，落点为B′．点B′从点A开始沿AD移动，折痕所在直线l的位置也随之改变，当直线l经过点A时，点B′停止移动，连接BB′．设直线l与AB相交于点E，与CD所在直线相交于点F，点B′的移动距离为x，点F与点C的距离为y．

    （1）求证：∠BEF=∠AB′B；

    （2）求y与x的函数关系式，并直接写出x的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    在△ABC中，点D是AB边的中点，点E是AC边的中点，连接DE，若BC=4，则DE=　

    查看答案和解析>>

    同步练习册答案