
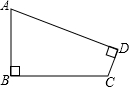
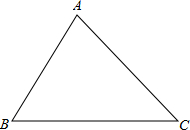
 如图四边形草坪ABCD,∠B=∠D=90°,AB=20cm,BC=15cm,CD=7cm.求这块草坪的面积.
如图四边形草坪ABCD,∠B=∠D=90°,AB=20cm,BC=15cm,CD=7cm.求这块草坪的面积.  科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:阅读理解
查看答案和解析>>
科目:初中数学 来源: 题型:
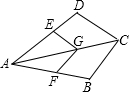
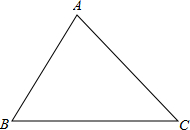
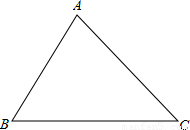
 5、小明和小东经常在一块三角形的草坪上玩耍,一天他们发现了一个有趣的现象,如图,草坪三角形ABC,他们两人同时从BC边的点P出发,小明沿与AC平行的线段PD(点D在AB上)、DA走向A处,小东沿与AC平行的线段PE(点D在AC上)、EA走向A处,当他们俩步行的速度相同时,他们同时到达A点,并且即使在BC边上改变P点的位置,当他们俩步行的速度一样时,到达A处的时间也完全一样,理由是
5、小明和小东经常在一块三角形的草坪上玩耍,一天他们发现了一个有趣的现象,如图,草坪三角形ABC,他们两人同时从BC边的点P出发,小明沿与AC平行的线段PD(点D在AB上)、DA走向A处,小东沿与AC平行的线段PE(点D在AC上)、EA走向A处,当他们俩步行的速度相同时,他们同时到达A点,并且即使在BC边上改变P点的位置,当他们俩步行的速度一样时,到达A处的时间也完全一样,理由是查看答案和解析>>
科目:初中数学 来源: 题型:
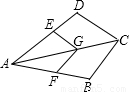
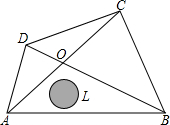 羊城雕塑公园草坪中有一湖,饲养黑天鹅等珍禽,如图,四边形ABCD表示公园,L表示“天鹅湖”.已知△ABC、△ABD、△COD的面积分别是42、40和12公顷,公园陆地总面积是61公顷,那么“天鹅湖”的面积是( )公顷.
羊城雕塑公园草坪中有一湖,饲养黑天鹅等珍禽,如图,四边形ABCD表示公园,L表示“天鹅湖”.已知△ABC、△ABD、△COD的面积分别是42、40和12公顷,公园陆地总面积是61公顷,那么“天鹅湖”的面积是( )公顷.| A、10 | B、9.5 | C、9 | D、8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2004年陕西省西安市高新一中中考数学模拟试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com