
| 73 |
| 8 |


 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
| ||
| 3 |
| 3 |

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
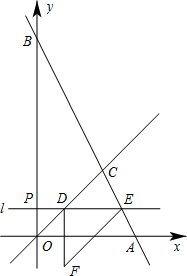 (2012•金东区一模)已知:如图,直线y=kx+b与x轴交于点A(8,0),与y轴交于点B(0,16),与直线y=x相交于点C.P(0,t)是y轴上的一个动点,过点P作直线l垂直y轴,与直线y=x相交于点D,与直线y=kx+b相交于点E,在直线l下方作一个等腰直角三角形DEF,使DF=DE,∠EDF=90°.
(2012•金东区一模)已知:如图,直线y=kx+b与x轴交于点A(8,0),与y轴交于点B(0,16),与直线y=x相交于点C.P(0,t)是y轴上的一个动点,过点P作直线l垂直y轴,与直线y=x相交于点D,与直线y=kx+b相交于点E,在直线l下方作一个等腰直角三角形DEF,使DF=DE,∠EDF=90°.查看答案和解析>>
科目:初中数学 来源: 题型:
 某居民小区要在一块一边靠墙(墙长13m)的空地上建一个矩形花园ABCD,花园一边靠墙,另三边用总长为20m的栅栏围成.如图,设AB=x(m),
某居民小区要在一块一边靠墙(墙长13m)的空地上建一个矩形花园ABCD,花园一边靠墙,另三边用总长为20m的栅栏围成.如图,设AB=x(m),查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com