
����Ŀ���Ķ�������ϣ�
����ѧ���ϣ���ʦ��ͬѧ˼���������⣺��ͼ1�����ǰ�һ���ı���ABCD���ı��е�E��F��G��H�������������õ����ı���EFGH��ƽ���ı�����
С����˼������ʱ��������˼·������AC��

���С����˼·������
��1����ֻ�ı�ͼ1���ı���ABCD����״����ͼ2�������ı���EFGH����ƽ���ı�����˵���������ο�С��˼���������������һ��������
��2����ͼ2���ڣ�1���������£�������AC��BD��
�ٵ�AC��BD����ʲô����ʱ���ı���EFGH�����Σ�д�����۲�֤����
�ڵ�AC��BD����ʲô����ʱ���ı���EFGH�Ǿ��Σ�ֱ��д�����ۣ�

���𰸡���1����ƽ���ı�������2����AC=BD����AC��BD��
��������
�����������1����ͼ2������AC��������������λ�ߵ�������ƽ���ı����ж��������ɵõ����ۣ�

��2�����ɣ�1��֪���ı���EFGH��ƽ���ı��Σ���FG=![]() BD��HG=
BD��HG=![]() AC�����ǵõ���AC=BDʱ��FG=HG�����ɵõ����ۣ�
AC�����ǵõ���AC=BDʱ��FG=HG�����ɵõ����ۣ�
�����ı���EFGH�Ǿ���������HGF=90�㣬��GH��GF����GH��AC��GF��BD����AC��BD��
�����������1����ƽ���ı�����֤��������
��ͼ2������AC����E��AB���е㣬F��BC���е㣬��EF��AC��EF=![]() AC��ͬ��HG��AC��HG=
AC��ͬ��HG��AC��HG=![]() AC�����Ͽɵã�EF��HG��EF=HG�����ı���EFGH��ƽ���ı��Σ�
AC�����Ͽɵã�EF��HG��EF=HG�����ı���EFGH��ƽ���ı��Σ�
��2����AC=BD��
�������£�
�ɣ�1��֪���ı���EFGH��ƽ���ı��Σ���FG=![]() BD��HG=
BD��HG=![]() AC���൱AC=BDʱ��FG=HG����ƽ���ı���EFGH��������
AC���൱AC=BDʱ��FG=HG����ƽ���ı���EFGH��������
����AC��BDʱ���ı���EFGHΪ���Σ�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ�ž���ֽ�尴ͼ�����߲ü��ɾſ飬�����������DZ߳���Ϊ![]() �Ĵ������Σ������DZ߳���Ϊ
�Ĵ������Σ������DZ߳���Ϊ![]() ��С�����Σ�����dz�Ϊ
��С�����Σ�����dz�Ϊ![]() ����Ϊ
����Ϊ![]() ��ȫ��С���Σ���
��ȫ��С���Σ���![]() >
> ![]() �������ϳ��ȵ�λ��cm��
�������ϳ��ȵ�λ��cm��
��1���۲�ͼ�Σ����Է��ִ���ʽ![]() ������ʽ�ֽ�Ϊ ��
������ʽ�ֽ�Ϊ ��
��2����ÿ��С���ε����Ϊ10![]() ���ĸ������ε������Ϊ58
���ĸ������ε������Ϊ58![]() ������ͼ�����вü��ߣ����߲��֣���֮�ͣ�
������ͼ�����вü��ߣ����߲��֣���֮�ͣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ڳ������º��������꣬ijˮ�����ˮ����ʱ������Ӷ����٣���֪ԭ����ˮ��y1����m3����ɺ�����ʱ��x���죩�Ĺ�ϵ��ͼ���߶�l1��ʾ��������ָɺ�������ӵ�10�쿪ʼ��ˮ��עˮ��עˮ��y2����m3����ʱ��x���죩�Ĺ�ϵ��ͼ���߶�l2��ʾ���������������أ���
��1����ԭ����ˮ��y1����m3����ɺ�����ʱ��x���죩�ĺ�����ϵʽ������x��10ʱ��ˮ������ˮ����
��2����0��x��50ʱ��ˮ�������ˮ��y����m3����ʱ��x���죩�ĺ�����ϵʽ��ע��x �ķ�Χ����������ˮ��������840��m3Ϊ���ظɺ���ֱ��д���������ظɺ�ʱx�ķ�Χ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η��̣�a2��1��x2+3ax��3��0��һ������x��1����a��ֵ��_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�ִ������������0.36%,����뱾��100Ԫ,��Ϣ��(��������Ϣ�ĺ�)y(Ԫ)����������x֮��ĺ�����ϵʽ��������5���º�ı�Ϣ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����˫����y=![]() ��y=��
��y=��![]() �ֱ�λ�ڵ�һ�������ޣ�A��y��������һ�㣬B��y=��
�ֱ�λ�ڵ�һ�������ޣ�A��y��������һ�㣬B��y=��![]() �ϵĵ㣬C��y=
�ϵĵ㣬C��y=![]() �ϵĵ㣬�߶�BC��x���ڵ� D����4BD=3CD��������˵������˫����y=
�ϵĵ㣬�߶�BC��x���ڵ� D����4BD=3CD��������˵������˫����y=![]() ��ÿ�������ڣ�y��x���������С��������B�ĺ�����Ϊ3�����C������Ϊ��3����
��ÿ�������ڣ�y��x���������С��������B�ĺ�����Ϊ3�����C������Ϊ��3����![]() ������k=4���ܡ�ABC�����Ϊ��ֵ7����ȷ���У��� ��
������k=4���ܡ�ABC�����Ϊ��ֵ7����ȷ���У��� ��
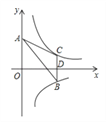
A. B. C. D. ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�AB=4��BC=6��EΪAB�е㣬����P�ӵ�B��ʼ��BC�����˶�����Cֹͣ������Q�ӵ�C��ʼ��CD��DA�����˶������Pͬʱ������ͬʱֹͣ����������˶��ٶȾ�Ϊÿ��1����λ���������ǵ��˶�ʱ��Ϊx���룩����EPQ�����Ϊy����y��x֮��ĺ�����ϵ��ͼ������ǣ� ��
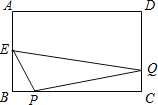
A��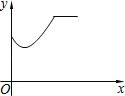 B��
B��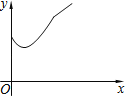 C��
C�� D��
D��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���߳�Ϊ2a�ĵȱ�������ABC�У�M�Ǹ�CH����ֱ���ϵ�һ�����㣬����MB�����߶�BM�Ƶ�B��ʱ����ת60��õ�BN������HN�����ڵ�M�˶������У��߶�HN���ȵ���Сֵ�ǣ� ��
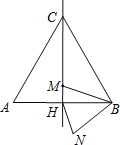
A��![]() a B��a C��
a B��a C��![]() D��
D��![]()
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com