
| x | �� | -1 | 0 | 3 | �� |
| y | �� | 0 | 3/2 | 0 | �� |
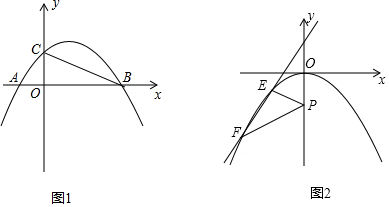
���� ��1����������y=-$\frac{1}{2}$x2+bx+c��x�ύ��A��B���㣬��-1��0������3��0����������������ߵĽ���ʽ��
��2������ȡOB���е�P��$\frac{3}{2}$��0��������CP��Ȼ�����P��PQ��BC����������Q����Ϊ�����������ֱ��BC�Ľ���ʽ��Ȼ����ƽ���ߵ����ʣ����ֱ��PQ�Ľ���ʽ��������$\left\{\begin{array}{l}{y=-\frac{1}{2}x+\frac{3}{4}}\\{y=-\frac{1}{2}{x}^{2}+x+\frac{3}{2}}\end{array}\right.$��������ô𰸣�
��3�����ȵõ�ƽ�ƺ�������ߵĽ���ʽΪ��y=-$\frac{1}{2}$x2���ٹ���E��EM��y����M������F��FN��y����N����Rt��EPM��Rt��FPN��������$\left\{\begin{array}{l}{y=kx+b}\\{y=-\frac{1}{2}{x}^{2}}\end{array}\right.$��������ô𰸣�
��� �⣺��1����������y=-$\frac{1}{2}$x2+bx+c��x�ύ��A��B���㣬��-1��0������3��0����
��y=-$\frac{1}{2}$��x+1����x-3����
�������ߵĽ���ʽΪ��y=-$\frac{1}{2}$x2+x+$\frac{3}{2}$�� ��2��ȡOB���е�P��$\frac{3}{2}$��0��������CP��
��2��ȡOB���е�P��$\frac{3}{2}$��0��������CP��
��S��PBC=$\frac{1}{2}$S��BOC��
����P��PQ��BC����������Q��������
����������y�ύ�ڵ�C��
���C����������0��$\frac{3}{2}$����
��ֱ��BC�Ľ���ʽΪy=kx+b��
$\left\{\begin{array}{l}{b=\frac{3}{2}}\\{3k+b=0}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=\frac{3}{2}}\end{array}\right.$��
��ֱ��BC�Ľ���ʽΪy=-$\frac{1}{2}$x+$\frac{3}{2}$��
����ֱ��PQ�Ľ���ʽΪy=-$\frac{1}{2}$x+n��
��-$\frac{1}{2}$��$\frac{3}{2}$+n=0��
��n=$\frac{3}{4}$��
��ֱ��PQ�Ľ���ʽΪy=-$\frac{1}{2}$x+$\frac{3}{4}$��
����$\left\{\begin{array}{l}{y=-\frac{1}{2}x+\frac{3}{4}}\\{y=-\frac{1}{2}{x}^{2}+x+\frac{3}{2}}\end{array}\right.$��
��ã�x=$\frac{-3��\sqrt{3}}{2}$��
��S��BCQ��$\frac{1}{2}$S��BOC
��xQ��ȡֵ��ΧΪ��xQ��$\frac{-3+\sqrt{3}}{2}$��xQ��$\frac{-3-\sqrt{3}}{2}$�� ��3��ƽ�ƺ�������ߵĽ���ʽΪ��y=-$\frac{1}{2}$x2��
��3��ƽ�ƺ�������ߵĽ���ʽΪ��y=-$\frac{1}{2}$x2��
����E��EM��y����M������F��FN��y����N��
�ɷ����֪����EPM=��FPN��
��Rt��EPM��Rt��FPN��
��$\frac{KM}{FN}$=$\frac{PM}{PN}$��
��E��x1��y1����F��x2��y2������ֱ��EF�Ľ���ʽΪy=kx+b��
��$\frac{-{x}_{1}}{-{x}_{2}}$=$\frac{{y}_{1}+1}{-1-{y}_{2}}$��
��x1��1+y2��+x2��y1+1��=0��
����$\left\{\begin{array}{l}{y=kx+b}\\{y=-\frac{1}{2}{x}^{2}}\end{array}\right.$��
������x2+2kx+2b=0��
��x1+x2=-2k��x1x2=2b��
��x1��1+y2��+x2��y1+1��=x1��1+kx2+b��+x2��kx1+b+1��=0��
��2bx1x2+��b+1����x1+x2��=0��
��2kb-2k=0��b=1��
��ֱ��EF�Ľ���ʽΪy=kx+1
��ֱ��EF�Ĺ����㣨0��1����
���� �������ڶ��κ������ۺ��⣮���������������ε��ж������ʡ�����ϵ���������Ľ���ʽ�Լ������Ľ������⣮ע��ȷ�����������ǽ����Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
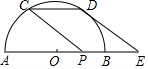 ��ͼ����֪��ԲO��ֱ��ABΪ8��PΪOB���е㣬CΪ��Բ��һ�㣬����CP������CP������AB����ƽ����DE����DEǡ�����O�����ڵ�D����ƽ�Ƶľ���Ϊ$\sqrt{33}$-1��
��ͼ����֪��ԲO��ֱ��ABΪ8��PΪOB���е㣬CΪ��Բ��һ�㣬����CP������CP������AB����ƽ����DE����DEǡ�����O�����ڵ�D����ƽ�Ƶľ���Ϊ$\sqrt{33}$-1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0��1 | B�� | 1��2 | C�� | 2��3 | D�� | 3��4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com