
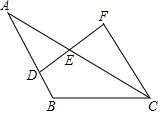
 如图,已知AB∥CF,E为DF的中点,若AB=13cm,CF=9cm,则BD=4cm.
如图,已知AB∥CF,E为DF的中点,若AB=13cm,CF=9cm,则BD=4cm. 科目:初中数学 来源: 题型:解答题
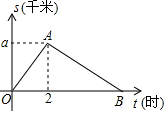 平顶山市教育局举行'重走长征路”健步活动,某教师从起点体育村沿建设路到市生态园.再沿原路返回.该教师离开起点的路程S(千米)与步行时间t(小时)之间的函数关系如图所示.其中从起点到市生态园的平均速度是4千米/小时.用2小时.根据图象提供信息.解答下列问题
平顶山市教育局举行'重走长征路”健步活动,某教师从起点体育村沿建设路到市生态园.再沿原路返回.该教师离开起点的路程S(千米)与步行时间t(小时)之间的函数关系如图所示.其中从起点到市生态园的平均速度是4千米/小时.用2小时.根据图象提供信息.解答下列问题查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
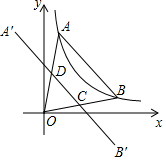 如图,点A、B在函数y=$\frac{1}{x}$(x>0)的图象上,点A在点B的左侧,且OA=OB,点A关于y轴的对称点为A′,点B关于x轴的对称点为B′,连接A′B′分别交OA、OB于点D、C.若四边形ABCD的面积为$\frac{6}{5}$,则点A的坐标为($\frac{1}{2}$,2),点C的坐标为($\frac{6}{5}$,$\frac{3}{10}$).
如图,点A、B在函数y=$\frac{1}{x}$(x>0)的图象上,点A在点B的左侧,且OA=OB,点A关于y轴的对称点为A′,点B关于x轴的对称点为B′,连接A′B′分别交OA、OB于点D、C.若四边形ABCD的面积为$\frac{6}{5}$,则点A的坐标为($\frac{1}{2}$,2),点C的坐标为($\frac{6}{5}$,$\frac{3}{10}$).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com