
【题目】如图,二次函数y=(x﹣3)2+m的图象与y轴交于点C,点B是点C关于该二次函数图象的对称轴对称的点,已知一次函数y=kx+b的图象经过该二次函数图象上的点A(1,0)及点B.
(1)求二次函数与一次函数的解析式;
(2)抛物线上是否存在一点P,使S△ABP=S△ABC?若存在,请求出点P的坐标,若不存在,请说明理由.
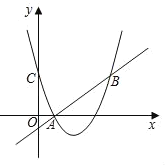
【答案】(1)y=(x﹣3)2﹣4;y=x﹣1;(2)存在,P点坐标为(3,﹣4)或(4,﹣3)或(7,12).
【解析】
(1)先将点A(1,0)代入y=(x﹣3)2+m求出m的值,根据点的对称性确定B点坐标,然后根据待定系数法求出一次函数解析式;
(2)假设存在点P,设点P(a,a2﹣6a+5),根据三角形ABP面积为三角形ABC面积,由两三角形都以AB为底边,得到C到直线AB的距离为P到直线AB距离相等,利用点到直线的距离公式列出关于a的方程,求出方程的解得到a的值,即可确定出满足题意P的坐标.
(1)将点A(1,0)代入y=(x﹣3)2+m得(1﹣3)2+m=0,解得:m=﹣4.
所以二次函数解析式为y=(x﹣3)2﹣4,即y=x2﹣6x+5;
当x=0时,y=9﹣4=5,所以C点坐标为(0,5),由于C和B关于对称轴对称,而抛物线的对称轴为直线x=3,所以B点坐标为(6,5),将A(1,0)、B(6,5)代入y=kx+b得:![]() ,解得:
,解得:![]() .
.
所以一次函数解析式为y=x﹣1;
(2)假设存在点P,设点P(a,a2﹣6a+5).
∵S△ABP=S△ABC,∴C到直线AB的距离为P到直线AB距离相等,∴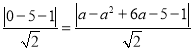 ,即﹣a2+7a﹣6=6或﹣a2+7a﹣6=﹣6,解得:a=3,a=4或a=0(舍去),a=7,则a2﹣6a+5=﹣4或﹣3或12,∴P点坐标为(3,﹣4)或(4,﹣3)或(7,12).
,即﹣a2+7a﹣6=6或﹣a2+7a﹣6=﹣6,解得:a=3,a=4或a=0(舍去),a=7,则a2﹣6a+5=﹣4或﹣3或12,∴P点坐标为(3,﹣4)或(4,﹣3)或(7,12).


 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
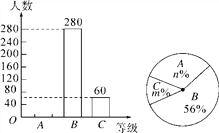
【题目】某报社为了解市民对“社会主义核心价值观”的知晓程度,采取随机抽样的方式进行问卷调查,调查结果分为“A.非常了解”、“B.了解”、“C.基本了解”三个等级,并根据调查结果绘制了如下两幅不完整的统计图.
(1)这次调查的市民人数为________人,m=________,n=________;
(2)补全条形统计图;
(3)若该市约有市民100000人,请你根据抽样调查的结果,估计该市大约有多少人对“社会主义核心价值观”达到“A.非常了解”的程度.
查看答案和解析>>
科目:初中数学 来源: 题型:
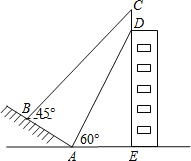
【题目】如图,山坡AB的坡度i=1:![]() ,AB=10米,AE=15米.在高楼的顶端竖立一块倒计时牌CD,在点B处测量计时牌的顶端C的仰角是45°,在点A处测量计时牌的底端D的仰角是60°,求这块倒计时牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米,参考数据:
,AB=10米,AE=15米.在高楼的顶端竖立一块倒计时牌CD,在点B处测量计时牌的顶端C的仰角是45°,在点A处测量计时牌的底端D的仰角是60°,求这块倒计时牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米,参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),顶点坐标是(1,n),与y轴的交点在(0,3)和(0,6)之间(包含端点),则下列结论错误的是( )
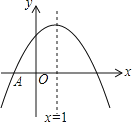
A.3a+b<0B.﹣2≤a≤﹣lC.abc>0D.9a+3b+2c>0
查看答案和解析>>
科目:初中数学 来源: 题型:
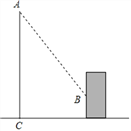
【题目】小左同学想利用影长测量学校旗杆的高度,如图,她在某一时刻立一长度为1米的标杆,测得其影长为![]() 米,同时旗杆投影的一部分在地上,另一部分在某一建筑物的墙上,测得旗杆与建筑物的距离为10米,旗杆在墙上的影高为2米,请帮小左同学算出学校旗杆的高度.
米,同时旗杆投影的一部分在地上,另一部分在某一建筑物的墙上,测得旗杆与建筑物的距离为10米,旗杆在墙上的影高为2米,请帮小左同学算出学校旗杆的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题8分)如图,在五边形ABCDE中,∠BCD=∠EDC=90°,BC=ED,AC=AD.
(1)求证:△ABC≌△AED;
(2)当∠B=140°时,求∠BAE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,设客车离甲地的距离为y1千米,出租车离甲地的距离为y2千米,两车行驶的时间为x小时,y1、y2关于x的函数图像如下图
所示:
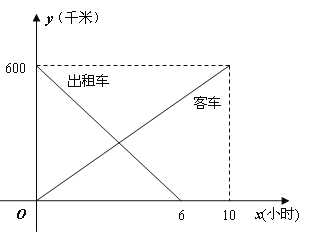
(1)根据图像,直接写出y1、y2关于x的函数关系式;
(2)若两车之间的距离为S千米,请写出S关于x的函数关系式;
(3)甲、乙两地间有A、B两个加油站,相距200千米,若客车进入A加油站时,出租车恰好进入B加油站,求A加油站离甲地的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com