
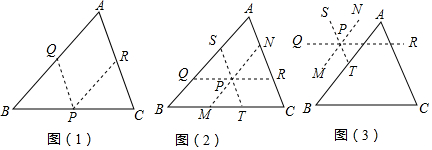
分析 如图1,把三个内角“凑”到BC边上的一点P,通过作平行线作出与三角形的角相等的角进行证明;如图2,可以把角“凑”到三角形的内部,即通过作平行线作出与三角形的角相等的角进行证明;如图3,可以把角“凑”到三角形的外部,即通过作平行线作出与三角形的角相等的角进行证明;还可以过△ABC某一顶点作对边的平行线进行证明.
解答 解:(1)可以,如图1,过BC上任一点P,作PQ∥AC,交AB于Q,作PR∥AB交AC于R,
则∠A=∠BQP=∠QPR,∠B=∠RPC,∠C=∠BPQ,
由∠BPQ+∠QPR+∠CPR=180°,可得∠A+∠B+∠C=180°;
(2)可以,如图2,过△ABC内任一点P作QR∥BC,作MN∥AB,作ST∥AC,
则∠A=∠QSP=∠SPN,∠B=∠SQP=∠NPR,∠C=∠NRP=∠QPS,
由∠SPQ+∠SPN+∠NPR=180°,可得∠A+∠B+∠C=180°;
(3)可以,如图3,过三角形外一点P分别作三角形三边的平行线,
则∠A=∠PTD=∠SPN,∠B=∠TDP=∠NPR,∠C=∠AED=∠QPS,
由∠SPQ+∠SPN+∠NPR=180°,可得∠A+∠B+∠C=180°;
(4)如图4,过△ABC的顶点C作CE∥AB,延长BC至D,
则∠1=∠B,∠2=∠A,
由∠ACB+∠1+∠2=180°,可得∠A+∠B+∠ACB=180°.
点评 本题考查的是平行线的性质以及平角定义的运用,根据题意作出辅助线,构造出平行线是解答此题的关键.


 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
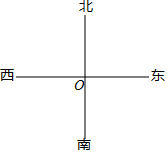 如图所示,一只蚂蚁从O点出发,沿北偏东60°方向爬行1.1cm,碰到一障碍物B后,又沿西北方向爬行1.6cm到C处.
如图所示,一只蚂蚁从O点出发,沿北偏东60°方向爬行1.1cm,碰到一障碍物B后,又沿西北方向爬行1.6cm到C处.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
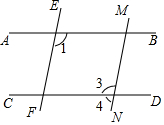 如图,直线AB,CD被直线EF,MN所截.
如图,直线AB,CD被直线EF,MN所截.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com